Kezdőlap


Feladat:	4443. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Gnädig Péter , Szabó Attila , Trócsányi Péter
Füzet:	2013/január, 46 - 48. oldal		PDF \| MathML
Témakör(ök):	Feladat, Felületi feszültségből származó erő, Felületi feszültségből származó energia
Hivatkozás(ok):	Feladatok: 2012/április: 4443. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Tekintsük a jobb oldali hártya kiszúrása után kialakuló egyensúlyi állapotot! A bal oldali hártya a felületi feszültség miatt kicsit összehúzódik, ettől a hajszál megfeszül és meggörbül. Ha a hajszál valamely részén a görbületi sugár

R

, és a hajszálban ébredő feszítőerő

F

, a közöttük fennálló kapcsolat:

\begin{matrix} F = σ R, \end{matrix}

(1)

ahol

σ

a hártya teljes (annak mindkét oldalát figyelembe vevő) felületi feszültsége. Ezt az összefüggést pl. a hajszál egy kicsiny,

Δ α

középponti szöggel jellemezhető, tehát

R Δ α

hosszú darabkájára felírt erőegyensúly egyenletéből kaphatjuk meg (1. ábra):

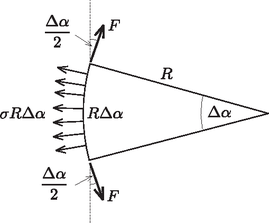\begin{matrix} 2 F sin \frac{Δ α}{2} \approx 2 F \frac{Δ α}{2} \approx σ R Δ α . \end{matrix}

1. ábra

2. ábra

Mivel a hajszál súlya elhanyagolható, az

F

feszítőerő a szál minden pontjában ugyanakkora kell legyen, így az (1) egyenlet szerint a görbületi sugár is mindenhol ugyanakkora. A szál tehát körív alakú lesz.
Legyen e körív középponti szöge

2 α

, sugara pedig

R

(2. ábra). Az ábráról leolvasható, hogy a körívhez tartozó húr hossza

\begin{matrix} ℓ = 2 R sin α, \end{matrix}

(2)

a megnyúlt hajszál hossza a körív ívhossza:

\begin{matrix} ℓ + Δ ℓ = 2 R α, \end{matrix}

vagyis a szál megnyúlása

\begin{matrix} Δ ℓ = 2 R (α - sin α) . \end{matrix}

(3)

Feltételezhetjük, hogy a szál megnyúlása és ezzel együtt az

α

szög is igen kicsiny, így alkalmazható a feladat szövegében megadott közelítés. Emiatt a szál megnyúlása ‐ a (2) összefüggés

ℓ \approx 2 R α

alakját is felhasználva ‐ így írható:

\begin{matrix} Δ ℓ = \frac{ℓ}{6} α^{2} . \end{matrix}

(4)

A hajszálban ható érintő irányú erő kifejezhető megnyúlással:

\begin{matrix} F = \frac{E A Δ ℓ}{ℓ}, \end{matrix}

ahonnan (1), (2) közelítő alakja és (4) felhasználásával a kérdéses szögre

\begin{matrix} α = \sqrt[3]{\frac{3 ℓ σ}{E A}}, \end{matrix}

a hajszál megnyúlására pedig

\begin{matrix} Δ ℓ = \frac{ℓ}{6} {(\frac{3 ℓ σ}{E A})}^{\frac{2}{3}} \end{matrix}

végeredmény adódik.

II. megoldás. A feladat megoldható az energiaminimum elve alapján is. Az egyik hártya átszúrása után kialakuló egyensúlyi állapotban a teljes energiája (ami a felületi feszültségből származó

E_{f}

energia és a megfeszülő hajszál

E_{r}

rugalmas energiájának összege) minimális kell legyen:

\begin{matrix} E_{t} = E_{f} + E_{r} = minimum. \end{matrix}

Az I. megoldás 2. ábrájának jelöléseit használva a felületi energia:

\begin{matrix} E_{f} = σ t, \end{matrix}

ahol

\begin{matrix} t = {(\frac{ℓ}{2})}^{2} \frac{π}{2} - R^{2} (α - sin α cos α) \end{matrix}

az épen maradt (az ábrán szürkén jelölt) hártya területe. Mivel (a megadott közelítő formula szerint)

\begin{matrix} sin α cos α = \frac{1}{2} sin (2 α) \approx \frac{1}{2} (2 α - \frac{1}{6} {(2 α)}^{3}) = α - \frac{2}{3} α^{3}, \end{matrix}

továbbá

R \approx ℓ / (2 α)

, a hártya felületi energiája az

α

szög függvényében:

\begin{matrix} E_{f} (α) = E_{0} - \frac{ℓ^{2} σ}{6} α . \end{matrix}

(Itt

E_{0}

egy konstans, tehát az energiaminimum szempontjából érdektelen állandó.)
A megfeszített hajszálban létrejövő rugalmas feszítőerő

\begin{matrix} F = \frac{E A}{ℓ} Δ ℓ, \end{matrix}

vagyis éppen akkora, mint egy

D = \frac{E A}{ℓ}

rugóállandójú rugóban ébredő erő. A rugalmas energia a rugó megfelelő képletének felhasználásával számolható:

\begin{matrix} E_{r} = \frac{1}{2} D {(Δ ℓ)}^{2} = \frac{E A}{2 ℓ} {(Δ ℓ)}^{2}, \end{matrix}

ami az I. megoldás (4) képletének felhasználásával így írható:

\begin{matrix} E_{r} = \frac{1}{72} E A ℓ α^{4} . \end{matrix}

A teljes energia:

\begin{matrix} E_{t} (α) = E_{0} - \frac{ℓ^{2} σ}{6} α + \frac{1}{72} E A ℓ α^{4}, \end{matrix}

melynek minimumát a derivált eltűnése adja meg:

\begin{matrix} E_{t}' (α) = - \frac{ℓ^{2} σ}{6} + \frac{1}{18} E A ℓ α^{3} = 0, \end{matrix}

vagyis az egyensúlyi állapotban

\begin{matrix} α = α_{0} = {(\frac{3 ℓ σ}{E A})}^{\frac{1}{3}}, \end{matrix}

a megnyúlás pedig

\begin{matrix} Δ ℓ = \frac{ℓ}{6} {(\frac{3 ℓ σ}{E A})}^{\frac{2}{3}}, \end{matrix}

összhangban az I. megoldás végeredményével.

Megjegyzés. Az egyensúlyi állapotban a rendszer energiája nem egyezik meg a jobb oldali hártya átszúrása utáni pillanatnak megfelelő ,,kezdeti'' energiával, vagyis

\begin{matrix} E_{t} (α_{0}) \neq E_{t} (α = 0) . \end{matrix}

Aki az energiamegmaradásra hivatkozva a felületi energia csökkenését a rugalmas energia növekedésével vette egyenlőnek, hibás eredményt kapott. Ténylegesen

| Δ E_{f} | = 4 \cdot Δ E_{r},

tehát a rendszer energiája az egyensúly beálltáig csökken.