Kezdőlap


Feladat:	4454. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	(W. B. T.) , Koncz Gabriella , Szabó Attila
Füzet:	2012/december, 562 - 566. oldal		PDF \| MathML
Témakör(ök):	Feladat, Fermat-elv, Egyéb fénytörés
Hivatkozás(ok):	Feladatok: 2012/május: 4454. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Két különböző optikai sűrűségű közeg határfelületén a fénysugarak megtörnek, a beesési merőlegestől való eltérésükre a Snellius‐Descartes-törvény (törési törvény) érvényes:

\begin{matrix} \frac{sin α_{1}}{sin α_{2}} = \frac{n_{2}}{n_{1}} . \end{matrix}

Ez az összefüggés általánosítható olyan esetekre is, amikor a törésmutató nem ugrásszerűen, hanem ‐ mint a jelen esetben is ‐ folytonosan változik.
Osszuk fel a változó törésmutatójú folyadékot gondolatban olyan vékony (vízszintes) rétegekre, hogy egy-egy rétegen belül az

n (h)

függvény változásától eltekinthessünk, vagyis egy-egy rétegen belül a törésmutatót (igen jó közelítéssel) állandónak tekinthessük.

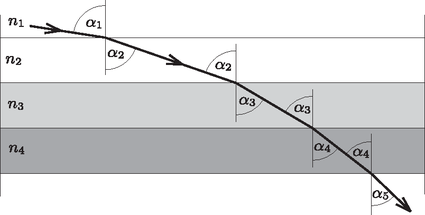1. ábra

Ekkor (az erősen eltorzított) 1. ábra jelöléseit követve felírhatjuk:

\begin{matrix} \frac{sin α_{1}}{sin α_{2}} = \frac{n_{2}}{n_{1}}, \frac{sin α_{2}}{sin α_{3}} = \frac{n_{3}}{n_{2}}, \frac{sin α_{3}}{sin α_{4}} = \frac{n_{4}}{n_{3}}, \frac{sin α_{4}}{sin α_{5}} = \frac{n_{5}}{n_{5}}, ..., \end{matrix}

vagyis

\begin{matrix} n_{1} sin α_{1} = n_{2} sin α_{2} = n_{3} sin α_{3} = n_{4} sin α_{4} = ... = állandó. \end{matrix}

Ezek szerint a folytonosan változó törésmutatójú folyadékban a fénysugár pályáját olyan görbe írja le, melynek tetszőleges pontjában a görbe meredekségét jellemző

φ = 90^{\circ} - α

szög és a kérdéses pontbeli törésmutató között fennáll:

\begin{matrix} n \cdot cos φ = állandó. \end{matrix}

(1)

A feladatban szereplő, kocka alakú akvárium szélessége

a = \sqrt[3]{V} = 0, 2 m

, és az edényben a magasság feléig, tehát 0,1 m-ig van víz. A törésmutató az akvárium alján

n_{0} = 1, 35

, az ,,ügyesen rétegzett'' sós víz legfelső rétegében pedig

\begin{matrix} n (h_{{max}_{}^{}}) = n_{0} - k h_{{max}_{}^{}}^{2} = 1, 35 - 2 \cdot 0, 1^{2} = 1, 33. \end{matrix}

Látható, hogy a törésmutató még az akvárium teljes vízmagassága mentén is csak nagyon kicsit változik, emiatt feltételezhetjük, hogy a vízszintesen érkező fénynyaláb minden fénysugara csak kicsit fog eltérni a vízszintestől. Ilyen esetekben alkalmazhatók az alábbi közelítések:

\begin{matrix} sin φ \approx tg φ \approx φ, illetve 1 - cos φ = 2 sin^{2} \frac{φ}{2} \approx 2 {(\frac{φ}{2})}^{2} = \frac{φ^{2}}{2} . \end{matrix}

(2)

Tekintsük azt a fénysugarat, amelyik

h_{0}

magasságban éri el (vízszintesen) az akvárium falát, majd fokozatosan elgörbülve valamekkora

h_{1}

magasságban,

φ_{{max}_{}^{}}

szögben haladva éri el az edény túlsó falát, és a vízszintestől mérve

γ

szögben hagyja el az akváriumot (2. ábra).

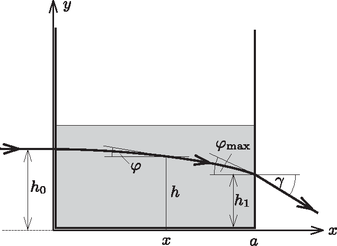2. ábra

A fénysugár menetét a meredekségére vonatkozó (1) összefüggés határozza meg. Ezt a görbe tetszőleges

(x, h)

koordinátájú pontjára felírva (és a törésmutató megadott magasságfüggését kihasználva) kapjuk:

n (h_{0}) = n (h) \cdot cos φ

, vagyis

\begin{matrix} n_{0} - k h_{0}^{2} = (n_{0} - k h^{2}) cos φ . \end{matrix}

(3)

Megjegyzés. Ez az összefüggés kapcsolatot teremt a

h (x)

egyenlettel megadott függvény és annak

φ

meredeksége között. Matematikai szempontból tehát egy differenciálegyenlettel van dolgunk, hiszen

h' (x) = - tg φ (x)

az ismeretlen függvény deriváltja. Ez a nehéz feladat azonban ‐ bizonyos közelítésekkel ‐ felsőbb matematikai ismeretek nélkül is megoldható.

Tételezzük fel, hogy a fénysugár menete parabolával közelíthető. (Ez nem teljesen megalapozatlan feltevés, hiszen minden ,,sima'' görbe elegendően kis környezetben egyenessel (az érintőjével), pontosabb (a hatványsorában másodrendű tagokig elmenő) számolásban pedig parabolával, vagy akár körrel (a simulókörrel) közelíthető.
Egy vízszintes érintővel,

h_{0}

magasságból induló parabola a 2. ábrán látható koordináta-rendszerben a

\begin{matrix} h (x) = h_{0} - K x^{2} \end{matrix}

(4)

egyenlettel írható le, ahol

K

egy később meghatározandó állandó. Ismert továbbá, hogy a parabola bármely pontjához tartozó érintő meredeksége éppen kétszerese a kérdéses pontot és a parabola csúcspontját összekötő szelő meredekségének.

Megjegyzés. Ez a geometriai tulajdonság jól látszik az ugyancsak parabolával szemléltethető

s (t) = a t^{2} / 2

egyenlettel leírható egyenletesen gyorsuló mozgás példáján. A megfogalmazott állítás itt annak felel meg, hogy a test pillanatnyi sebessége éppen kétszerese az indítástól számított átlagsebességének.)

Esetünkben ez annyit jelent, hogy

\begin{matrix} φ \approx tg φ = 2 \frac{h_{0} - h (x)}{x} = 2 \frac{K x^{2}}{x} = 2 K x . \end{matrix}

(5)

(Ugyanezt az eredményt a

h (x)

függvény deriválásával is megkaphatjuk, hiszen

- tg φ = h' (x) = - 2 K x

. ) Helyettesítsük be (4)-et (3)-ba, és használjuk fel a (2) közelítést is:

\begin{matrix} n_{0} - k h_{0}^{2} = (n_{0} - k {(h_{0} - K x^{2})}^{2}) (1 - \frac{φ^{2}}{2}), \end{matrix}

azaz

\begin{matrix} n_{0} - k h_{0}^{2} = n_{0} - k h_{0}^{2} + 2 k h_{0} K x^{2} + [k K^{2} x^{4}] - n_{0} \frac{φ^{2}}{2} + [k {(h_{0} - K x^{2})}^{2} \cdot \frac{φ^{2}}{2}] . \end{matrix}

(6)

Vegyük még figyelembe, hogy a fénysugár csak nagyon kicsit tér el a vízszintestől, így

φ ≪ 1

és

K x^{2} ≪ h_{0}

, továbbá a törésmutató változása is nagyon kicsi, tehát

k h_{0}^{2} ≪ n_{0} .

Emiatt a (6)-ban szereplő szögletes zárójeles kifejezések a többi tag mellett elhanyagolhatóak, s így az egyenlet lényegesen leegyszerűsödik:

\begin{matrix} 2 k K h_{0} x^{2} = n_{0} \frac{φ^{2}}{2}, \end{matrix}

vagyis (ha (5) alapján

φ

-t kifejezzük

x

-szel)

\begin{matrix} 2 k K h_{0} x^{2} = n_{0} \frac{4 K^{2} x^{2}}{2} . \end{matrix}

Ez minden

x

-re (tehát a fénysugár mentén mindenhol) teljesül, ha

K = \frac{k h_{0}}{n_{0}}

. Innen következik, hogy a fénysugár

\begin{matrix} h_{1} = h_{0} - K a^{2} = h_{0} (1 - \frac{k a^{2}}{n_{0}}) \approx h_{0} \end{matrix}

magasságban éri el az akvárium túlsó falát, beesési szöge pedig

\begin{matrix} φ_{{max}_{}^{}} = φ (x = a) = 2 \frac{k a h_{0}}{n_{0}} . \end{matrix}

Az akváriumból kilépő fénysugár megtörik, a törési szög a Snellius‐Descartes-törvény szerint

\begin{matrix} γ \approx sin γ = n_{0} \cdot sin φ_{{max}_{}^{}} \approx n_{0} \cdot φ_{{max}_{}^{}} = 2 k a h_{0} . \end{matrix}

(A törésmutató lassú változása és a fénysugár kicsiny eltérülése miatt a kilépés helyén a törésmutatót

n_{0}

-nak vettük.)
A

h_{0}

magasságban kilépő, a vízszinteshez képest

γ

szögben haladó fénysugár

\begin{matrix} d = \frac{h_{0}}{tg γ} \approx \frac{h_{0}}{γ} = \frac{1}{2 k a} = 1, 25 m \end{matrix}

távolságban éri el az akvárium fenéklapjának síkját. Ez a

d

távolság nem függ

h_{0}

-tól, tehát valamennyi fénysugárra ugyanakkora. Ezek szerint az akvárium úgy viselkedik, mint egy

d

fókusztávolságú (0,8 dioptriás) hengerlencse, a fókusztávolságnak megfelelő helyen levő ernyőn a fénynyalábot vékony, éles, vízszintes csíkká képezi le.
Ugyanerre az eredményre jutunk, ha a fénysugár menetét alkalmas sugarú körrel közelítjük, vagy ha a törési törvényből adódó (3) egyenletet numerikusan oldjuk meg, a folyadék vékony csíkokra bontásával (lásd az 1. ábrát).

II. megoldás. Vegyük észre, hogy a feladat megfogalmazása azt jelenti, hogy az akváriumban lévő sós víz fókuszálja az akvárium falára érkező párhuzamos fénynyalábot. A megoldás a Fermat-elv felhasználásán alapul, bizonyos közelítések felhasználásával. Azt használjuk ki, hogy fókuszálás esetében a megvilágító nyaláb fénysugarai ugyanakkora idő alatt érik el az ernyőt. (Ha ez nem így lenne, akkor a különböző idők alatt beérkező fényhullámok különböző fázisuk miatt kioltanák egymást.)

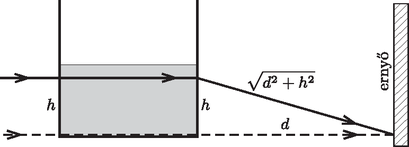3. ábra

A 3. ábra két különböző fénysugár útját mutatja, vázlatosan. A szaggatottan jelölt fénysugár a vízben (az akvárium alján) lassabban halad, azonban az akváriumot elhagyva, a levegőben rövidebb az útja. A felső fénysugár a vízben a kisebb törésmutató miatt gyorsabban halad, viszont a levegőben hosszabb utat kell megtennie. Az ábra azt is mutatja, hogy az ernyőn a fényes csík az akvárium aljával egy vonalban keletkezik. A kocka alakú akvárium térfogatából (8 liter) kiszámíthatjuk a kocka oldalélét:

a = 2 dm = 0, 2 m

.
Meggondolásunkban az a közelítés, hogy bár a fénysugarak már az akváriumban elhajlanak, az akváriumon történő áthaladás idejét úgy számítjuk ki, mintha a vízben mindvégig vízszintesen haladnának. A törésmutató változása miatt az akvárium úgy viselkedik, mint egy gyenge, félbevágott, félhenger alakú gyűjtőlencse.
Írjuk fel a két fénysugárra a megegyező áthaladási időt az akváriumba történő belépéstől az ernyő eléréséig:

\begin{matrix} a \cdot \frac{n_{0}}{c} + d \cdot \frac{1}{c} = a \cdot \frac{n_{0} - k h^{2}}{c} + \sqrt[]{d^{2} + h^{2}} \cdot \frac{1}{c}, \end{matrix}

ahol

c

a fénysebesség a levegőben,

d

pedig az akvárium és az ernyő távolsága. Az egyenlet átrendezése után ezt az alakot kapjuk:

\begin{matrix} d + a k h^{2} = \sqrt[]{d^{2} + h^{2}} . \end{matrix}

Mindkét oldal négyzetre emelésével tüntessük el a gyököt:

\begin{matrix} d^{2} + 2 a d k h^{2} + a^{2} k^{2} h^{4} = d^{2} + h^{2}, \end{matrix}

ami így is írható:

\begin{matrix} 2 a d k = 1 - {(a k h)}^{2} . \end{matrix}

Vegyük észre, hogy a jobb oldal második tagja sokkal kisebb 1-nél, tehát elhagyható, és emiatt

2 a d k = 1

, vagyis jó közelítéssel

\begin{matrix} d = \frac{1}{2 a k} = 1,25 m = 125 cm . \end{matrix}

Ezek szerint az akvárium úgy viselkedik, mint egy 0,8 dioptriás hengeres gyűjtőlencse.

Megjegyzés. Sajnálatos módon egy olyan ‐ nem túl régi ‐ versenyfeladat került kitűzésre, melynek megoldása az interneten közvetlenül elérhető volt. A KöMaL pontversenyének kiírása szerint ha valaki könyvekben vagy az interneten talált írásokat használ fel, és ezekből idéz, fel kell tüntetnie a forrásokat. Ennek elmulasztása (sokan követték el ezt a hibát) a modern tudományos, műszaki vagy irodalmi életben plágiumnak minősül! Célunk továbbra is versenyzőink problémamegoldó képességének fejlesztése, nem pedig a keresőprogramok tesztelése.