Kezdőlap


Feladat:	4436. fizika feladat	Korcsoport: 14-15	Nehézségi fok: átlagos
Megoldó(k):	Demeter Dániel , Feher Zsombor , Papp Roland , Vajda Balázs
Füzet:	2012/szeptember, 373 - 375. oldal		PDF \| MathML
Témakör(ök):	Feladat, Földrajzzal kapcsolatos feladatok, Coriolis-erő
Hivatkozás(ok):	Feladatok: 2012/április: 4436. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás.

a)

A sétahajó negyedóra alatt

\begin{matrix} s = v t = 18 \frac{km}{h} \cdot \frac{1 h}{4} = 4, 5 km \end{matrix}

utat tesz meg. A hosszúsági körök ívei egyenlő hosszúak, így különbség csak a nyugat-keleti és kelet-nyugati ívek hosszában lesz.
Siófok az északi szélesség

φ = {46, 91}^{\circ}

-án található. Egy délkör hossza közelítőleg 40 000 km; a 4,5 km-es észak-dél irányú elmozdulás tehát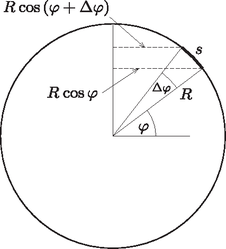

\begin{matrix} Δ φ = \frac{4, 5}{40 000} \cdot 360^{\circ} \approx {0, 04}^{\circ} \end{matrix}

változást jelent a szélességi koordinátában (1. ábra).

1. ábra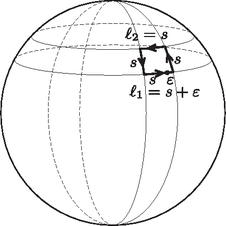

2. ábra

Azonos délkörök közötti, de különböző szélességi köríveken történő elmozdulások hosszának aránya (lásd a 2. ábrát):

\begin{matrix} \frac{ℓ_{1}}{ℓ_{2}} = \frac{R cos φ}{R cos (φ + Δ φ)} = \frac{cos {46, 91}^{\circ}}{cos {46, 95}^{\circ}} = 1, 000 75. \end{matrix}

Az északabbra eső kelet-nyugat irányú elmozdulás ívének hossza ismert:

ℓ_{2} = s = 4,5

km, ebből kiszámítható, hogy a délebbre eső ív hossza

ℓ_{1} = 4503, 4

méter lenne. Ha a hajó körbeért volna, éppen ekkora távolságot kellett volna megtennie. Mivel csak 4500 métert tett meg kelet felé, az út végén

ε = ℓ_{1} - ℓ_{2} \approx 3, 4

méternyire került a kiindulási helyétől, nyugatra.

Megjegyzés. Az

ε

távolság összemérhető a sétahajó méreteivel, így a kezdeti és a végső helyzet távolsága csak a hajó valamely kitüntetett, az irányváltoztatás során el nem mozduló pontjára értelmezhető.

b)

A Földhöz képes mozgó testek súlyának megváltozását az inerciarendszerhez viszonyított

a

gyorsulás megváltozásával magyarázhatjuk. A Newton-féle mozgásegyenlet szerint:

\begin{matrix} F_{g} + K = m a, \end{matrix}

ahol

F_{g}

a testre ható gravitációs erő,

K

pedig az alátámasztást biztosító kényszererő (jelen esetben ez a Balaton vizének felhajtóereje).
A test súlya ‐ megállapodás szerint ‐ a kényszererő nagyságával egyenlő: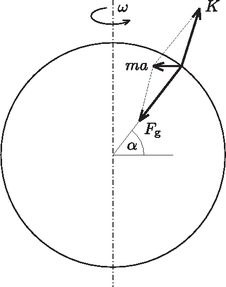

\begin{matrix} G = | K | = | F_{g} - m a |, \end{matrix}

ami egy

α

szélességi körön kelet felé

v

sebességgel mozgó,

m

tömegű test estén így számolható (lásd a 3. ábrát):

\begin{matrix} G = \sqrt[]{{(F_{g} sin α)}^{2} + {(F_{g} cos α - m a)}^{2}} . \end{matrix}

3. ábra

A test sebessége inerciarendszerben a Föld forgásából adódó

R ω cos α

kerületi sebesség és

v

előjeles összege, pályasugara

r = R cos α

, gyorsulása tehát

\begin{matrix} a = \frac{{(R ω cos α + v)}^{2}}{r} . \end{matrix}

Az Egyenlítő hossza kb.

K = 40 075

km. Siófok szélességi körének kerülete (ha a Föld alakjának a gömbtől való eltérését nem vesszük figyelembe):

\begin{matrix} K_{1} = K cos {46, 91}^{\circ} = 27 377 km, \end{matrix}

az ennek megfelelő sugár pedig

\begin{matrix} r_{1} = \frac{K_{1}}{2 π} = 4357, 2 km . \end{matrix}

T = 24 h

periódusidővel forgó Föld kerületi sebessége ezen a helyen

\begin{matrix} V_{1} = \frac{K_{1}}{T} = \frac{27 377 km}{86 400 s} = 316, 86 \frac{m}{s} . \end{matrix}

A kelet felé haladó hajó sebessége hozzáadódik a Föld felszínének (ugyancsak kelet felé mutató) sebességéhez, nagysága tehát

\begin{matrix} v_{1} = V_{1} + v = 316, 86 \frac{m}{s} + 5 \frac{m}{s} = 321, 86 \frac{m}{s}, \end{matrix}

a test centripetális gyorsulása pedig

\begin{matrix} a_{1} = \frac{v_{1}^{2}}{r_{1}} = 0, 023 77 \frac{m}{s^{2}} . \end{matrix}

Ezeket az értékeket (

m = 50 000

kg és

α = {46, 91}^{\circ}

adatokat is kihasználva) a súlyt megadó képletbe helyettesítve

\begin{matrix} G_{1} = 489 688 N \end{matrix}

adódik.
Ismételjük meg a számolást a Siófoktól északra, attól 5 km távolságban húzódó szélességi kör mentén nyugat felé mozgó, tehát

v = - 5 \frac{m}{s}

sebességű hajóra! A szélességi kör kerülete

\begin{matrix} K_{2} = K cos {46, 95}^{\circ} = 27 356 km, \end{matrix}

a megfelelő sugár

\begin{matrix} r_{2} = \frac{K_{2}}{2 π} = 4353, 9 km, \end{matrix}

a Föld felszínének kerületi sebessége ezen a helyen

\begin{matrix} V_{2} = \frac{K_{2}}{T} = 316, 62 \frac{m}{s}, \end{matrix}

a hajó sebessége (inerciarendszerben, kelet felé)

\begin{matrix} v_{2} = 316, 62 \frac{m}{s} - 5 \frac{m}{s} = 311, 62 \frac{m}{s}, \end{matrix}

centripetális gyorsulása tehát

\begin{matrix} a_{2} = \frac{v_{2}^{2}}{r_{2}} = 0, 022 30 \frac{m}{s^{2}} . \end{matrix}

A hajó súlya ebben az esetben

\begin{matrix} G_{2} = 489 740 N. \end{matrix}

Látható, hogy a kelet felé haladó hajó súlya mintegy 52 N-nal kisebb, mint az ugyanekkora sebességgel nyugati irányban mozgó hajóé.

Megjegyzések. 1. A megoldásban a gravitációs erőt az

F_{g} = m g

képlet alapján, a szokásos

g = 9, 81 m / s^{2}

értékkel számoltuk, jóllehet ez a mennyiség már tartalmazza a Föld forgásából adódó kicsiny korrekciót. Eljárásunk mégis helyes, mert a súlykülönbség számításánál a gravitációs erőnek megfelelő legnagyobb tag kiesik, nem lényeges tehát, ha azt kicsit ,,pontatlanul'' számoljuk.
2. A Föld alakja ténylegesen eltér a gömbtől, emiatt a hajó súlya még akkor is különböző lenne két különböző szélességi kör mentén, ha a sétahajó a vízhez képest nem mozogna. Ez a különbség azonban lényegesen kisebb, mint a feladatban számolt (a hajó mozgásából adódó) érték.
3. Eötvös Loránd (1848‐1919) magyarázta meg és mutatta ki kísérletileg is, hogy a Földön kelet felé mozgó testek súlya kisebb, mint a nyugat felé mozgóké. Tiszteletére ezt a jelenséget Eötvös-effektusnak nevezik.