Kezdőlap


Feladat:	4394. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Gnädig Péter , Tardos Jakab
Füzet:	2012/május, 299 - 303. oldal		PDF \| MathML
Témakör(ök):	Feladat, Pontrendszerek mozgásegyenletei
Hivatkozás(ok):	Feladatok: 2011/december: 4394. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.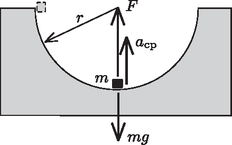

I. megoldás.

a)

Legyen a félhenger sugara

r

, és a helyzeti energiát tekintsük a pálya legalsó pontjánánál nullának. A mechanikai energiamegmaradás törvénye szerint az

m

tömegű test

v

sebessége a pálya legmélyebb pontján így számolható:

\begin{matrix} m g r & = \frac{1}{2} m v^{2}, \\ v^{2} & = 2 g r . \end{matrix}

A Newton-egyenlet szerint a kis test és a hasáb között ható erő

F

erő a kérdéses pontban (1. ábra):

\begin{matrix} F - m g = m a_{cp}, ahol a_{cp} = \frac{v^{2}}{r}, \end{matrix}

innen

\begin{matrix} F = m g + m \frac{v^{2}}{r} = m g + 2 m g = 3 m g . \end{matrix}

1. ábra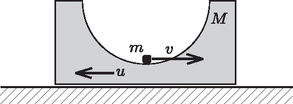

2. ábra

b)

Vizsgáljuk most azt az esetet, amikor a hasáb nem rögzített, hanem súrlódásmentesen elcsúszhat a vízszintes felületen! Jelöljük az

m

tömegű test sebességét a pálya legalján

v

-vel, a

M

tömegű hasáb sebességét pedig

u

-val (2. ábra)! (A két test sebessége egymással ellentétes irányú.) Mivel a rendszerre nem hat olyan külső erő, aminek vízszintes komponense nullától különböző lenne, a rendszer összlendületének vízszintes komponense mindvégig, így a vizsgálandó pillanatban is nulla kell legyen:

\begin{matrix} M u - m v & = 0, \\ M u & = m v . \end{matrix}

A mechanikai energiamegmaradás tételét alkalmazhatjuk az

m

és

M

tömegű testekből álló redszerre:

\begin{matrix} m g r & = \frac{1}{2} m v^{2} + \frac{1}{2} M u^{2}, \\ 2 m g r & = m v^{2} + M u^{2}, \\ 2 m g r & = m v^{2} + m u v, \\ 2 g r & = u v + v^{2} . \end{matrix}

Abban a pillanatban, amikor az

m

tömegű test a pályája legalsó pontján van, tekinthetjük az

M

tömegű testet tehetetlenségi (gyorsulásmentes) vonatkoztatási rendszernek.

Megjegyzés. A hasábhoz rögzített koordináta-rendszer gyorsuló rendszer, amelyben ‐ eredeti alakjukban ‐ nem érvényesek a Newton-törvények. Abban a pillanatban azonban, amikor

v

és vele együtt

u

a legnagyobb értékét veszi fel, a koordináta-rendszer gyorsulása éppen nulla, tehát a hasáb vonatkoztatási rendszere inerciarendszernek tekinthető.

Ebből a vonatkoztatási rendszerből nézve a kis test

v_{relatív} = u + v

sebességgel

r

sugarú körpályán mozog, centripetális gyorsulása tehát:

\begin{matrix} a_{cp} = \frac{{(u + v)}^{2}}{r} . \end{matrix}

Írjuk fel az

m

tömegű testre a pálya legmélyebb pontján (ahol a hasábra kifejtett erő

F

erő a megadott

3, 5 m g

nagyságú) a Newton-féle mozgásegyenlet:

\begin{matrix} F - m g & = m a_{cp}, \\ 3, 5 m g - m g & = m \frac{{(u + v)}^{2}}{r}, \\ 2, 5 g & = \frac{{(u + v)}^{2}}{r}, \\ u + v & = \sqrt[]{2, 5 r g} . \end{matrix}

Használjuk fel az energiamegmaradásból kapott eredményt is:

\begin{matrix} \frac{u v + v^{2}}{u + v} = \frac{2 r g}{\sqrt[]{2, 5 r g}}, \end{matrix}

vagyis a kis test sebessége a pálya mélypontján:

\begin{matrix} v = \sqrt[]{\frac{8}{5} r g} . \end{matrix}

Ebből a hasáb sebessége is megkapható:

\begin{matrix} u = \sqrt[]{\frac{5}{2} r g} - v = \sqrt[]{\frac{5}{2} r g} - \sqrt[]{\frac{8}{5} r g} = \sqrt[]{\frac{1}{10} r g}, \end{matrix}

és végül a tömegek aránya is kiszámítható:

\begin{matrix} \frac{m}{M} = \frac{u}{v} = \frac{1}{4} . \end{matrix}

A hasáb tömege tehát négyszer akkora, mint a kis testé.

II. megoldás. Számítsuk ki a két test közötti

F

nyomóerő nagyságát tetszőleges

m / M

tömegarányra! Ebből

m ≪ M

határesetben az

a)

kérdésre kapunk választ, a

b)

kérdésnél pedig az

F = 3, 5 m g

adatból a tömegarányt határozhatjuk meg.
Írjuk le a mozgást az álló, vízszintes felülethez rögzített inerciarendszerből! Vízszintes irányú külső erők hiányában a rendszer tömegközéppontja vízszintesen nem mozdulhat el, fennáll tehát, hogy

\begin{matrix} m x = M X, \end{matrix}

ahol

x

a kis test távolsága a tömegközépponton átmenő függőleges egyenestől,

X

pedig ugyanez a mennyiség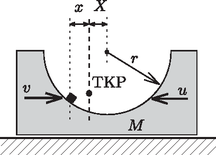

a hasábra vonatkoztatva (3. ábra). Innen következik, hogy a

v = - \frac{Δ x}{Δ t}

és

u = - \frac{Δ X}{Δ t}

sebességek aránya is a tömegaránnyal egyenlő:

\begin{matrix} m v = M u, azaz \frac{u}{v} = \frac{m}{M} . \end{matrix}

(Az előjelválasztás az I. megoldásban használt jelöléseknek felel meg.)

3. ábra

A mechanikai energiamegmaradás törvényéből következik, hogy a kis test pályájának legmélyebb helyzetében

\begin{matrix} \frac{1}{2} m v^{2} + \frac{1}{2} M u^{2} = \frac{1}{2} m v^{2} (1 + \frac{M}{m} \cdot \frac{u^{2}}{v^{2}}) = m g r, \end{matrix}

ahonnan a sebességarányok ismeretében adódik, hogy

\begin{matrix} \frac{1}{2} m v^{2} (1 + \frac{m}{M}) = m g r, \end{matrix}

vagyis

\begin{matrix} v = \sqrt[]{2 g r} \cdot \sqrt[]{\frac{M}{M + m}} . \end{matrix}

Vajon milyen pályán mozog a kis test a választott vonatkoztatási rendszerből nézve? Abban a helyzetben, amikor a kis test a tömegközépponttól vízszintes irányban mérve

x

távolságra van, a henger középpontja

X = \frac{m}{M} x

messze lesz a tömegközépponton átmenő függőleges egyenestől. Ha ebben a helyzetben a kis test függőleges irányú elmozdulása

y

, akkor fenn kell álljon a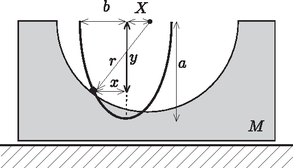

\begin{matrix} {(x + X)}^{2} + y^{2} = r^{2} \end{matrix}

kényszerfeltétel (hiszen a kis test rajta kell legyen a félhenger palástján). Innen

X

-et

x

-szel kifejezve az

\begin{matrix} {(\frac{x}{a})}^{2} + {(\frac{y}{b})}^{2} = 1 \end{matrix}

összefüggés, vagyis egy ellipszis egyenlete adódik (4. ábra), ahol a féltengelyek hossza:

\begin{matrix} a = r és b = \frac{M}{M + m} r . \end{matrix}

4. ábra

A pálya legmélyebb pontjában, vagyis az ellipszis csúcspontjában a pálya görbületi sugara:

\begin{matrix} ϱ = \frac{b^{2}}{a} = {(\frac{M}{M + m})}^{2} r . \end{matrix}

Megjegyzés. A görbületi sugár képlete pl. úgy is származtatható, hogy egy tömegpont ‐ amelynek mozgása két, egymásra merőleges irányú harmonikus rezgőmozgásból tevődik össze ‐ gyorsulását kétfeleképpen is kiszámítjuk. Legyen

\begin{matrix} x (t) = a cos ω t, y (t) = b sin ω t, \end{matrix}

ekkor

t = 0

pillanatban a test sebessége

v = b ω

, gyorsulásának nagysága pedig egyrészt

a ω^{2}

, másrészt

v^{2} / ϱ

alakban is felírható. Innen az ellipszis görbületi sugara (simulókörének sugara) a nagytengely végpontjaiban:

\begin{matrix} ϱ = \frac{v^{2}}{a ω^{2}} = \frac{b^{2}}{a} . \end{matrix}

A Newton-féle mozgásegyenlet felhasználásával kiszámíthatjuk a kis test és a hasáb között ható

F

erőt a pálya legalsó pontjában:

\begin{matrix} F - m g = m \frac{v^{2}}{ϱ}, \end{matrix}

azaz

\begin{matrix} F = m g + m \cdot 2 g r \frac{M}{M + m} \cdot {(\frac{M + m}{M})}^{2} \frac{1}{r} = m g (3 + 2 \frac{m}{M}) . \end{matrix}

Innen már egyszerűen adódik, hogy ha

m ≪ M

, akkor

F = 3 m g

, és az

F = 3, 5 m g

érték

M = 4 m

esetén valósul meg.