Kezdőlap


Feladat:	4331. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Gnädig Péter , Vigh Máté
Füzet:	2011/november, 502 - 504. oldal		PDF \| MathML
Témakör(ök):	Feladat, Görbületi nyomás, Egyéb felületi feszültség
Hivatkozás(ok):	Feladatok: 2011/március: 4331. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az egyensúlyi állapotot pl. az energiaminimum-elv segítségével találhatjuk meg. Súlytalanság állapotában a gravitációs helyzeti energia figyelmen kívül hagyható, elegendő a felületi energiákkal foglalkoznunk. Bár a feladat szövegéből nem derül ki egyértelműen, hogy a gömbben a vízen kívül még mi van, feltételezzük, hogy ott normál állapotú levegő található.
$a)$ Az üveget jól (,,tökéletesen'') nedvesítő víz számára energetikailag az a kedvező, ha minél nagyobb felületen érintkezik az edény falával. Mivel a gravitáció nem szab gátat ennek, a víz az üreges gömb teljes belső felületét benedvesíti, a légbuborék tehát valahol az üreg belsejében fog elhelyezkedni. Alakját az a feltétel szabja meg, hogy a felülete ‐ adott térfogat mellett ‐ a lehető legkisebb legyen. (A térfogat azért állandó, mert a normál légnyomás mellett a felületi feszültségből származó nyomás elhanyagolhatóan kicsi, tehát a gáznak a nyomása és a hőmérséklete, és így a térfogata is meghatározott értékű.)
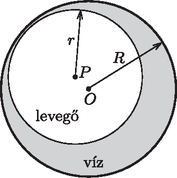
Adott térfogatú testek közül a gömbnek a legkisebb a felszíne (ezt már az ókorban is tudták). Az $R = 4$ cm sugarú üregbe bezárt levegő tehát gömb alakú lesz (1. ábra). A gömb $r$ sugarát a térfogatából számolhatjuk ki:

\begin{matrix} \frac{4 r^{3} π}{3} = \frac{2}{3} \cdot \frac{4 R^{3} π}{3}, ahonnan r = \sqrt[3]{\frac{2}{3}} R = 3, 5 cm . \end{matrix}

A légbuborék

O

középpontja tetszőleges lehet, az egyensúly tehát

O

helyzetére nézve közömbös (indifferens). A buborék az üreges edényben a legkisebb hatásra (pl. az űrállomás nagyon kicsi fékeződésére) lassan mozoghat, de az edény falához érve onnan visszapattan, nem ,,ragad'' oda.

1. ábra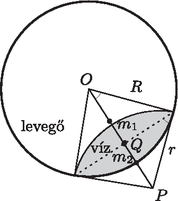

2. ábra

Megjegyzés. A gömb alakú felület minden pontjának ugyanakkora a görbülete, és ennek megfelelően a légbuborék falánál mindenhol ugyanakkora a felületi feszültségből származó görbületi nyomása. Ennek így is kell lennie, hiszen a belül levő gáz nyomása is és a külső víz nyomása is (súlytalanság állapotában) a felület mentén haladva nem változik; különbségük pedig éppen a görbületi nyomás.

b)

Az ezüstgömbbe zárt légbuborék is olyan alakot vesz fel,
amelynek átlagos görbülete,

\frac{1}{2} (\frac{1}{R_{max}} + \frac{1}{R_{min}})

a felület minden pontjában ugyanakkora (hiszen a levegő nyomása is és a víz nyomása is állandó a felület mentén), és a határán az érintősíkja mindenhol merőleges a falfelület érintősíkjára. Ezt a két feltételt a gömbsüveg (a gömbfelületnek egy síkkal ,,levágott'' része) ‐ ha alkalmasan választjuk meg a méretét és a középpontjának helyzetét ‐ nyilván teljesíti, a gömbsüveg tehát egy lehetséges megoldás. Mivel azonban a matematikai probléma megoldása ‐ fizikai okokból ‐ egyértelmű, ez lesz a megoldás: az edényben levő víz (,,vízpogácsa'') két gömbsüvegből összetehető alakot vesz fel (2. ábra).

Megjegyzés. A folyadék és a levegő határfelülete általában nem gömbfelület, vagy annak egy darabkája, hanem bonyolultabb (konstans átlaggörbületű) alakzat. Ha például az űrállomáson lebegő tartály ürege nem gömb, hanem szabálytalan alakú lenne, akkor az üreg szélénél összegyűlő vízet nem határolhatná gömbfelület; annak érintősíkjai ugyanis nem mindenhol ugyanakkora szögben illeszkednének a falfelülethez. Feladatunkban azért lehetséges egy viszonylag egyszerű felülettel, a gömbsüveggel kielégíteni a szükséges feltételeket, mert két gömb áthatásakor a felületek közös része mentén az érintősíkok szöge mindenhol ugyanakkora.

A határfelület

r

görbületi sugarát és

P

középpontjának az üreges gömb

O

középpontjától mért távolságát a víz térfogata és az illeszkedési szög határozza meg. Mivel a Pitagorasz-tétel, valamint hasonló háromszögek arányai miatt fennáll

\begin{matrix} O P = \sqrt[]{R^{2} + r^{2}}, O Q = \frac{R^{2}}{\sqrt[]{R^{2} + r^{2}}} és P Q = \frac{r^{2}}{\sqrt[]{R^{2} + r^{2}}}, \end{matrix}

a 3. ábrán látható gömbsüvegek magassága:

\begin{matrix} m_{1} = r (1 - \frac{r}{\sqrt[]{R^{2} + r^{2}}}), m_{2} = R (1 - \frac{R}{\sqrt[]{R^{2} + r^{2}}}) . \end{matrix}

Táblázati képletek szerint egy

ϱ

sugarú,

m

magasságú gömbsüveg térfogata

\frac{π}{3} m^{2} (3 ϱ - m)

, így a víz ismert térfogata

\begin{matrix} \frac{π}{3} m_{1}^{2} (3 r - m_{1}) + \frac{π}{3} m_{2}^{2} (3 R - m_{2}) = \frac{1}{3} \cdot \frac{4 π}{3} R^{3} \end{matrix}

módon fejezhető ki. Innen az

x = r / R

sugár-arányra az

\begin{matrix} x^{3} {(1 - \frac{x}{\sqrt[]{1 + x^{2}}})}^{2} (2 + \frac{x}{\sqrt[]{1 + x^{2}}}) + {(1 - \frac{1}{\sqrt[]{1 + x^{2}}})}^{2} (2 + \frac{1}{\sqrt[]{1 + x^{2}}}) = \frac{4}{3} \end{matrix}

egyenlet adódik, amelynek (numerikusan, vagy grafikus függvényábrázolással megkapható) megoldása:

x = 3, 205 \approx 3, 2

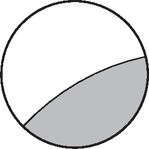3. ábra

A vizet tehát egy

r = 12, 8

cm sugarú gömbsüveg alakú felület választja el a levegőtől; méretarányos rajza a 3. ábrán látható. A vízpogácsa állása a súlytalanság miatt tetszőleges lehet. Elvben elképzelhető, hogy a légbuborék ebben az esetben is az 1. ábrán látható gömb alakú és valahol a gömb belsejében lebeg, de ez az állapot instabil. Ha a buborék ‐ bármilyen kis zavar hatására ‐ megközelíti az edény falát, onnan nem pattan vissza (mint az

a)

esetben), hanem rátapad a falra. Kiszámítható, hogy a felületi energia számottevően kisebb a 3. ábrán látható elrendezésben, mint az 1. ábrának megfelelőben. (Az energiaviszonyok könnyen összehasonlíthatóak egy sík felületre tapadó buboréknál.) Itt egy gömbből vele azonos térfogatú félgömb lesz, ennek felülete

1 / \sqrt[3]{2} \approx 0, 8

-szor kisebb a gömbénél.