Feladat:	4301. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Horicsányi Attila ,  Laczkó Zoltán Balázs
Füzet:	2011/május, 302 - 304. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Newton-féle gravitációs erő, Gravitációs helyzeti energia
Hivatkozás(ok):	Feladatok: 2010/december: 4301. fizika feladat

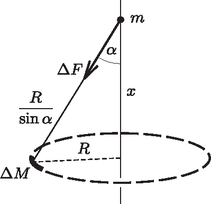
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. $a)$ Számítsuk ki, hogy mekkora gravitációs erőt fejt ki a gyűrű a tengelye mentén elhelyezkedő $m$ tömegű testre, ha az a gyűrű síkjától $x$ távolságra található. Osszuk fel gondolatban a gyűrűt kicsiny, pontszerűnek tekinthető $\Delta M$ tömegű darabkákra! Minden egyes darabka ugyanakkora, $\frac{R}{\text{sin}\alpha }$ távolságra van a $m$ tömegű testtől, ahol az ábrán látható $\alpha$ szögre $\text{tg}\alpha =\frac{R}{x}$.     Az egyes gyűrűdarabkák által kifejtett gravitációs vonzóerő nagysága $\begin{array}{c}{\displaystyle \Delta F=f\frac{m\Delta M\text{sin}{}^2\alpha }{R^2}\mathrm{.}}\end{array}$ Ezen erőknek a gyűrű síkjába eső komponensei (szimmetria-okok miatt) kiegyenlítik egymást, az összegük nulla. A tengely irányú komponensek viszont összeadódnak, és az eredőjük: $\begin{array}{c}{\displaystyle F=\sum \Delta F\text{cos}\alpha =f\frac{m(\sum \Delta M)\text{sin}{}^2\alpha \text{cos}\alpha }{R^2}=f\frac{mM\text{sin}{}^2\alpha \text{cos}\alpha }{R^2}\mathrm{.}}\end{array}$ Ez az erő ott maximális, ahol a $\text{sin}{}^2\alpha \text{cos}\alpha$ kifejezés a legnagyobb értékű. Számítógéppel (vagy akár egy zsebszámológéppel) számolva könnyen megállapíthatjuk, hogy (hegyesszögekre korlátozódva) a maximum ${\alpha }_{\text{m}}\approx 54\mathrm{,}{7}^{\circ }$-nál található. Ennek megfelelően a gravitációs térerősség a gyűrű síkjától $\begin{array}{c}{\displaystyle x_{\text{m}}=\frac{R}{\text{tg}{\alpha }_{\text{m}}}\approx 0\mathrm{,}71R}\end{array}$ távolságban lesz maximális nagyságú. $b)$ A gyűrűből és a $m$ tömegű testből álló rendszer összenergiája (a gravitációs energia és a mozgási energiák összege) a mozgás során állandó marad. A tömegekre megadott feltétel miatt a (kezdetben állónak tekintett) gyűrű gyakorlatilag mozdulatlan marad, mozgási energiája a másik test mozgási energiája mellett elhanyagolható. Pontszerű, egymástól $r$ távol levő testek gravitációs helyzeti energiáját az $\begin{array}{c}{\displaystyle E_{\text{g}}=-f\frac{m_1{m}_2}{r}}\end{array}$ összefüggés alapján számíthatjuk ki. Jelen esetben (mivel a gyűrű minden darabkája ugyanolyan messze van a tengely mentén mozgó kis testtől) a fenti képlet $\begin{array}{c}{\displaystyle m_1=m\mathrm{,}{m}_2=M\mathrm{,}{r}_{\text{kezdeti}}=\frac{R}{\text{sin}{\alpha }_{\text{m}}}\mathrm{,}{r}_{\text{végső}}=R}\end{array}$ helyettesítéssel alkalmazható. Az energiamegmaradás törvénye szerint $\begin{array}{c}{\displaystyle -f\frac{mM}{R}\text{sin}{\alpha }_{\text{m}}=\frac{1}{2}m{v}^2-f\frac{mM}{R}\mathrm{,}}\end{array}$ ahonnan a kis test sebessége a gyűrű középpontjánál $\begin{array}{c}{\displaystyle v=\sqrt[]{2\left(1-\text{sin}{\alpha }_{\text{m}}\right)\cdot f\frac{M}{R}}\approx \sqrt[]{0\mathrm{,}37\cdot f\frac{M}{R}}\approx 0\mathrm{,}61\sqrt[]{f\frac{M}{R}}\mathrm{.}}\end{array}$     II. megoldás. $a)$ Az I. megoldás jelöléseit követve a gravitációs gyorsulás a gyűrű síkjától $x$ távolságban: $\begin{array}{c}{\displaystyle g\left(x\right)=f\frac{M}{x^2+R^2}\cdot \text{cos}\alpha =fM\cdot \frac{x}{{\left(x^2+R^2\right)}^{3/2}}\mathrm{,}}\end{array}$ ami $\begin{array}{c}{\displaystyle g\left(x\right)=fM\cdot \frac{1}{{\left[x^{\frac{4}{3}}+R^2\cdot x^{-\frac{2}{3}}\right]}^{3/2}}}\end{array}$ alakra is hozható. Ennek a függvénynek ott van maximuma, ahol a szögletes zárójelben álló kifejezésnek minimuma, hiszen a számláló állandó, a $\frac{3}{2}$-ik hatványfüggvény pedig monoton növekvő. A minimum helyét a derivált eltűnéséből kaphatjuk meg: $\begin{array}{c}{\displaystyle \left(x^{\frac{4}{3}}+R^2\cdot x^{-\frac{2}{3}}\right)\text{'}=\frac{4}{3}\cdot x^{\frac{1}{3}}-\frac{2}{3}{R}^2\cdot x^{-\frac{5}{3}}=\mathrm{0,}}\end{array}$ ahonnan (az $x\ge 0$ tartományban) $\begin{array}{c}{\displaystyle x^2=\frac{R^2}{2}\mathrm{,}\text{azaz}x=\frac{R}{\sqrt[]{2}}\mathrm{.}}\end{array}$ (A második derivált a kérdéses helyen pozitív, tehát valóban minimumot találtunk.)   Megjegyzés. A szögletes zárójelben álló kifejezés legkisebb értékét differenciálszámítás nélkül, a számtani és mértani közepekre vonatkozó egyenlőtlenségből is megkaphatjuk: $\begin{array}{c}{\displaystyle \frac{x^{\frac{4}{3}}+R^2{x}^{-\frac{2}{3}}}{3}=\frac{x^{\frac{4}{3}}+\frac{R^2}{2}{x}^{-\frac{2}{3}}+\frac{R^2}{2}{x}^{-\frac{2}{3}}}{3}\ge \sqrt[3]{x^{\frac{4}{3}}\cdot \frac{R^2}{2}{x}^{-\frac{2}{3}}\cdot \frac{R^2}{2}{x}^{-\frac{2}{3}}}\mathrm{,}}\end{array}$ és az egyenlőség (a szélsőérték) éppen akkor teljesül, amikor az átlagolt mennyiségek megegyeznek: $\begin{array}{c}{\displaystyle x^{\frac{4}{3}}=\frac{R^2}{2}{x}^{-\frac{2}{3}}\mathrm{,}\text{tehát}x=\frac{R}{\sqrt[]{2}}\mathrm{.}}\end{array}$  (G. P.)   $b)$ A mozgás során ‐ külső erők hiányában ‐ az impulzus megmarad. Írjuk le a mozgást abban a koordináta-rendszerben, amelyben kezdetben a gyűrű is és a kis test is nyugalomban volt. Ha a $m$ tömegű test sebessége valamely pillanatban $v$, a gyűrűé pedig (ellentétes irányban) $V$, akkor az impulzusmegmaradás törvénye szerint $\begin{array}{c}{\displaystyle mv-MV=\mathrm{0,}\text{azaz}V=\frac{m}{M}v\mathrm{.}}\end{array}$ A két test együttes mozgási energiája: $\begin{array}{c}{\displaystyle \frac{1}{2}m{v}^2+\frac{1}{2}M{V}^2=\frac{1}{2}m{v}^2+\frac{1}{2}M\cdot \frac{m^2}{M^2}{v}^2=\frac{1}{2}m{v}^2\left(1+\frac{m}{M}\right)\approx \frac{1}{2}m{v}^2\mathrm{.}}\end{array}$ Látható, hogy a $m\ll M$ feltétel miatt a gyűrű mozgási energiája elhanyagolható a kis test mozgási energiája mellett. Az energiamegmaradás törvénye szerint a kezdeti (nyugalmi) állapotot és a gyűrű középpontján való áthaladás pillanatát összehasonlítva: $\begin{array}{c}{\displaystyle -f\frac{mM}{\sqrt[]{\frac{3}{2}}R}=\frac{1}{2}m{v}^2-f\frac{mM}{R}\mathrm{,}}\end{array}$ ahonnan az áthaladás sebességére $\begin{array}{c}{\displaystyle v=\sqrt[]{\frac{2fM}{R}\left(1-\sqrt[]{\frac{2}{3}}\right)}\approx 0\mathrm{,}606\sqrt[]{f\frac{M}{R}}}\end{array}$ adódik. (Kihasználtuk, hogy az induláskor a gyűrű minden része $\begin{array}{c}{\displaystyle \sqrt[]{R^2+x^2}=\sqrt[]{R^2+\frac{R^2}{2}}=\sqrt[]{\frac{3}{2}}R}\end{array}$ távolságra volt a $m$ tömegű testtől.)