Kezdőlap


Feladat:	4260. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Szabó Attila , Vigh Máté
Füzet:	2011/február, 107 - 110. oldal		PDF \| MathML
Témakör(ök):	Feladat, Pontrendszerek mozgásegyenletei
Hivatkozás(ok):	Feladatok: 2010/május: 4260. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Az 1. ábrán látható koordináta-rendszerben minden pillanatban teljesül a fonál nyújthatatlanságát kifejező

\begin{matrix} x^{2} + y^{2} = L^{2} \end{matrix}

(1)

kényszerfeltétel.

1. ábra

Kicsiny

Δ t

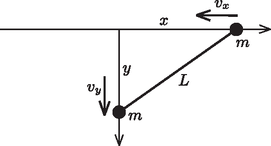idő elteltével is fennáll ugyanez, tehát

\begin{matrix} {(x - v_{x} Δ t)}^{2} + {(y + v_{y} Δ t)}^{2} = L^{2} . \end{matrix}

(2)

(

v_{x}

és

v_{y}

az egyes testek sebessége az ábrán látható irányítással.) A

Δ t

-ben másodfokú (másodrendűen kicsi) tagokat elhagyva a fenti két egyenletből

\begin{matrix} x v_{x} = y v_{y} \end{matrix}

(3)

adódik.

Megjegyzés. Ugyanezt az összefüggést úgy is megkaphatjuk, hogy felírjuk a testek sebességének fonál irányú vetületét, és kihasználjuk, hogy ezek nagysága ‐ a fonál hosszának állandósága miatt ‐ ugyanakkora kell legyen:

\begin{matrix} v_{x} \cdot \frac{x}{L} = v_{y} \cdot \frac{y}{L} . \end{matrix}

Most meghatározzuk a sebességeket az

y

koordináta függvényében. Szorítkozzunk először a rendszer mozgásának azon részére, amikor

v_{x} \geq 0

v_{y} \geq 0

és

x \geq 0

. A munkatételből következik, hogy

\begin{matrix} \frac{1}{2} m v_{x}^{2} + \frac{1}{2} m v_{y}^{2} = m g y . \end{matrix}

Ebből (1) és (3) felhasználásával

\begin{matrix} v_{x}^{2} + v_{x}^{2} \frac{x^{2}}{y^{2}} = 2 g y, \end{matrix}

vagyis

\begin{matrix} v_{x} = \frac{y}{L} \sqrt[]{2 g y} és v_{y} = \frac{x}{L} \sqrt[]{2 g y} \end{matrix}

adódik. Látható, hogy

v_{x}

y

monoton növekvő függvénye, így maximuma

y

legnagyobb,

y^{{max}_{}^{}} = L

értékéhez kötődik. Ekkor

v_{x}^{{max}_{}^{}} = \sqrt[]{2 g L} \approx 1, 41 \sqrt[]{g L}

.
Fejezzük ki

v_{y}

-t (1) felhasználásával csak

y

, vagy a dimenziótlan

u = \frac{y}{L}

függvényeként:

\begin{matrix} v_{y} = \sqrt[]{\frac{x^{2}}{L^{2}} 2 g y} = \sqrt[]{\frac{(L^{2} - y^{2}) 2 g y}{L^{2}}} = \sqrt[]{2 g L} \sqrt[]{(1 - u^{2}) u} . \end{matrix}

Ez a sebesség akkor a legnagyobb, amikor az

(1 - u^{2}) u

kifejezés értéke maximális. Differenciálszámítással, vagy a kifejezés numerikus kiszámításával és grafikus ábrázolással megkaphatjuk, hogy a szélsőérték

\begin{matrix} u = \frac{1}{\sqrt[]{3}} \approx 0, 58; y = \frac{L}{\sqrt[]{3}} \end{matrix}

értékhez tartozik, és ekkor

\begin{matrix} v_{y}^{{max}_{}^{}} = \sqrt[]{\frac{4 g L}{3 \sqrt[]{3}}} \approx 0, 88 \sqrt[]{g L} . \end{matrix}

Ekkora sebességekre gyorsulnak fel az egyes testek a nehézségi erő hatására.
A mozgás további szakaszában a vízszintesen mozgó test átlendül az origón, majd fokozatosan lassulva az

x = - L

helyzetben egy pillanatra megáll; ezután a mozgása folytatódik ,,visszafelé''. Mivel a testek sebességének nagysága egyértelműen meghatározható a helyzetük függvényében, így a mozgás periodikusan ismétlődő (anharmonikus) rezgőmozgás. A vízszintesen mozgó test periódusideje kétszer nagyobb, mint a függőlegesen mozgó testé.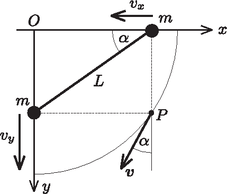

II. megoldás. Vegyük észre, hogy a 2. ábrán látható

P

pont a mozgás során mindvégig

L

távolságra van az

O

origótól, ezért egy

L

sugarú köríven mozog.

2. ábra

E pont

v

sebességének

x

irányú komponense (ha az előjelét ,,balra'' tekintjük pozitívnak) a felső test mindenkori

v_{x}

sebességével,

y

irányú komponense pedig az alsó test

v_{y}

sebességével egyezik meg. A mechanikai energia megmaradását kifejező

\begin{matrix} m g L sin α = \frac{1}{2} m v_{x}^{2} + \frac{1}{2} m v_{y}^{2} \end{matrix}

egyenlet ezért átírható

\begin{matrix} m g L sin α = \frac{1}{2} m v^{2} \end{matrix}

(4)

alakba, amely azt fejezi ki, hogy a

P

pont éppen úgy mozog, ahogy egy

L

hosszúságú, vízszintesen kitérített fonálinga mozog a nehézségi erő hatására.
A feladatnak arra a kérdésére, hogy hogyan mozognak a testek már most válaszolhatunk: a felső test úgy mozog, ahogy ennek az ingának a földön keletkező árnyéka mozog függőlegesen lefelé irányuló megvilágítás esetén; az alsó test pedig úgy, ahogy az oldalról megvilágított inga árnyéka mozog egy függőleges falon. Ebből következik, hogy a felső test sebessége akkor lesz legnagyobb, amikor éppen áthalad az origón, ekkor ugyanis

v

nagysága maximális, iránya pedig vízszintes. A (4) egyenletből leolvasható, hogy ez a sebesség

\begin{matrix} v_{x}^{{max}_{}^{}} = \sqrt[]{2 g L} . \end{matrix}

Az alsó test sebessége előbb növekszik, majd csökken. A

v_{y}

sebesség legnagyobb értékét akkor éri el, amikor az inga gyorsulásának függőleges komponense nullává válik. Ez a gyorsuláskomponens az inga érintő irányú (tangenciális)

a_{t}

és fonál irányú (centripetális)

a_{cp}

gyorsulásának megfelelő vetületeiből számítható ki:

\begin{matrix} a_{t} cos α - a_{cp} sin α = 0. \end{matrix}

(5)

Az inga érintő irányú gyorsulásának nagysága egy

α

szöggel jellemezhető helyzetben (a mozgásegyenlet szerint)

\begin{matrix} a_{t} = g cos α, \end{matrix}

a centripetális gyorsulása pedig (az energiamegmaradás tételéből számíthatóan)

\begin{matrix} a_{cp} = \frac{v^{2}}{L} = 2 g sin α . \end{matrix}

Ezeket (5)-be helyettesítve kapjuk, hogy az alsó test azon

α = α^{*}

szöggel jellemzett helyzetben mozog leggyorsabban, amikor

g cos^{2} α^{*} - 2 g sin^{2} α^{*} = 0

teljesül, vagyis

\begin{matrix} α^{*} = arctg \sqrt[]{2} / 2 = 35, 26^{\circ} . \end{matrix}

Az alsó test sebessége ebben a helyzetben:

\begin{matrix} v_{y}^{{max}_{}^{}} = v cos α^{*} = \sqrt[]{2 g L sin α^{*}} cos α^{*} \approx 0, 88 \sqrt[]{g L} . \end{matrix}