Kezdőlap


Feladat:	4258. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Lájer Márton , Neumer Tamás
Füzet:	2010/december, 564 - 566. oldal		PDF \| MathML
Témakör(ök):	Feladat, Erőrendszer eredője
Hivatkozás(ok):	Feladatok: 2010/május: 4258. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen a rudak hossza rendre $ℓ_{1}$ , $ℓ_{2}$ és $ℓ_{3}$ . A rudak páronkénti merőlegessége miatt az alátámasztási pontok távolsága a Pitagorasz-tétel szerint:

\begin{matrix} a = \sqrt[]{ℓ_{2}^{2} + ℓ_{3}^{2}}, b = \sqrt[]{ℓ_{1}^{2} + ℓ_{3}^{2}}, és c = \sqrt[]{ℓ_{1}^{2} + ℓ_{3}^{2}} . \end{matrix}

A test

Q

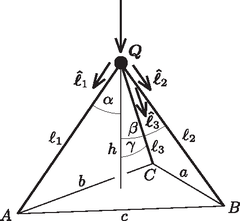
súlya rudakon úgy oszlik meg, hogy a rudakban ható (rúdirányú) erők vektori összege éppen

Q

-t adja vissza. Az ábrán látható jelölésekkel ez az erőfelbontás:

\begin{matrix} Q = {\hat{ℓ}}_{1} \cdot Q cos α + {\hat{ℓ}}_{2} \cdot Q cos β + {\hat{ℓ}}_{3} \cdot Q cos γ, \end{matrix}

ahol

{\hat{ℓ}}_{1}

{\hat{ℓ}}_{2}

és

{\hat{ℓ}}_{3}

a rudak irányába mutató egységvektorok. A rudak által alkotott tetraéder

h

magasságával kifejezve az erőfelbontás így is írható:

\begin{matrix} Q = {\hat{ℓ}}_{1} \cdot Q \frac{h}{ℓ_{1}} + {\hat{ℓ}}_{2} \cdot Q \frac{h}{ℓ_{2}} + {\hat{ℓ}}_{3} \cdot Q \frac{h}{ℓ_{3}} . \end{matrix}

Ebben a képletben az egységvektorok együtthatói éppen a kérdéses rúderők nagyságával egyeznek meg; megadásukhoz a

h

magasságot kell még kiszámítanunk.

Írjuk fel a tetraéder

V

térfogatát kétféle módon! Egyrészt az

ℓ_{1}

és

ℓ_{2}

hosszúságú rudak alkotta derékszögű háromszög területe

\frac{1}{2} ℓ_{2} ℓ_{2}

, így az

ℓ_{3}

magasságú tetraéder térfogata:

\begin{matrix} V = \frac{1}{3} \cdot \frac{1}{2} ℓ_{1} ℓ_{2} \cdot ℓ_{3} = \frac{ℓ_{1} ℓ_{2} ℓ_{3}}{6} . \end{matrix}

Másrészt a térfogat kifejezhető az

A B C

háromszög

T

területével és a

h

magassággal is:

\begin{matrix} V = \frac{1}{3} T h . \end{matrix}

A két alak összevetéséből

\begin{matrix} h = \frac{3 V}{T} = \frac{ℓ_{1} ℓ_{2} ℓ_{3}}{2 T} . \end{matrix}

A B C

háromszög

T

területe az oldalélek hosszának ismeretében a Heron-képletből számítható ki:

\begin{matrix} T = \sqrt[]{s (s - a) (s - b) (s - c)}, \end{matrix}

ahol

s = \frac{a + b + c}{2}

. Az oldaléleket a rudak hosszával kifejezve (algebrai átalakítások után) a terület így írható:

\begin{matrix} T = \frac{1}{2} \sqrt[]{ℓ_{1}^{2} ℓ_{2}^{2} + ℓ_{2}^{2} ℓ_{3}^{2} + ℓ_{3}^{2} ℓ_{1}^{2}}, \end{matrix}

a kérdéses magasság pedig

\begin{matrix} h = \frac{ℓ_{1} ℓ_{2} ℓ_{3}}{\sqrt[]{ℓ_{1}^{2} ℓ_{2}^{2} + ℓ_{2}^{2} ℓ_{3}^{2} + ℓ_{3}^{2} ℓ_{1}^{2}}} . \end{matrix}

A rudakban ható erők tehát:

\begin{matrix} F_{1} & = \frac{h}{ℓ_{1}} Q = \frac{ℓ_{2} ℓ_{3}}{\sqrt[]{ℓ_{1}^{2} ℓ_{2}^{2} + ℓ_{2}^{2} ℓ_{3}^{2} + ℓ_{3}^{2} ℓ_{1}^{2}}} Q = \frac{\frac{1}{ℓ_{1}}}{\sqrt[]{\frac{1}{ℓ_{1}^{2}} + \frac{1}{ℓ_{2}^{2}} + \frac{1}{ℓ_{3}^{2}}}} Q, \\ F_{2} & = \frac{h}{ℓ_{2}} Q = \frac{ℓ_{1} ℓ_{3}}{\sqrt[]{ℓ_{1}^{2} ℓ_{2}^{2} + ℓ_{2}^{2} ℓ_{3}^{2} + ℓ_{3}^{2} ℓ_{1}^{2}}} Q = \frac{\frac{1}{ℓ_{2}}}{\sqrt[]{\frac{1}{ℓ_{1}^{2}} + \frac{1}{ℓ_{2}^{2}} + \frac{1}{ℓ_{3}^{2}}}} Q, \\ és \\ F_{3} & = \frac{h}{ℓ_{3}} Q = \frac{ℓ_{1} ℓ_{2}}{\sqrt[]{ℓ_{1}^{2} ℓ_{2}^{2} + ℓ_{2}^{2} ℓ_{3}^{2} + ℓ_{3}^{2} ℓ_{1}^{2}}} Q = \frac{\frac{1}{ℓ_{3}}}{\sqrt[]{\frac{1}{ℓ_{1}^{2}} + \frac{1}{ℓ_{2}^{2}} + \frac{1}{ℓ_{3}^{2}}}} Q . \end{matrix}

Egyenlő hosszúságú rudak esetén

\begin{matrix} F_{1} = F_{2} = F_{3} = \frac{1}{\sqrt[]{3}} Q . \end{matrix}

II. megoldás. Egy-egy rúdban ébredő erő iránya rúdirányú kell legyen (ellenkező esetben az elhanyagolható súlyú és csuklós végpontú rúd elfordulna). A három rúd által a

Q

súlyú testre kifejtett erők eredőjének nagysága

Q

, iránya pedig a súlyerővel ellentétes kell legyen.
Tekintsük az általános,

a

b

és

c

hosszúságú rúd esetét! Jelöljük az

a

hosszúságú rúd függőlegessel bezárt szögét

α

-val, a másik két rúd és a függőleges szögét

β

-val és

γ

-val! A keresett rúderők nagysága:

\begin{matrix} Q_{a} = Q cos α, Q_{b} = Q cos β, Q_{c} = Q cos γ . \end{matrix}

A három (páronként derékszögű) rúdhoz koordináta-rendszert illeszthetünk. Az alátámasztás síkja

x = a

y = b

és

z = c

pontokban metszi a tengelyeket, a sík tengelymetszetes alakú egyenlete tehát

\begin{matrix} \frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1. \end{matrix}

Emellett fölírható a sík alaktényezős egyenlete is:

A x + B y + C z + D = 0

, ahol

\begin{matrix} A = \frac{1}{a}, B = \frac{1}{b} és C = \frac{1}{c}, \end{matrix}

továbbá

D = - 1

. Az

A = (A, B, C)

vektor, és a belőle képezhető

\begin{matrix} n = \frac{A}{| A |} = \frac{(A, B, C)}{\sqrt[]{A^{2} + B^{2} + C^{2}}} = \frac{(\frac{1}{a}, \frac{1}{b}, \frac{1}{c})}{\sqrt[]{\frac{1}{a^{2}} + \frac{1}{b^{2}} + \frac{1}{c^{2}}}} \end{matrix}

egységvektor merőleges az alátámasztás vízszintes síkjára, tehát függőleges irányú.
A függőleges egyenes és a koordinátatengelyek (vagyis a rudak) által bezárt szögek koszinuszai éppen az

n

vektor komponensei, vagyis

\begin{matrix} cos α & = \frac{\frac{1}{a}}{\sqrt[]{\frac{1}{a^{2}} + \frac{1}{b^{2}} + \frac{1}{c^{2}}}}, \\ cos β & = \frac{\frac{1}{b}}{\sqrt[]{\frac{1}{a^{2}} + \frac{1}{b^{2}} + \frac{1}{c^{2}}}}, \\ és \\ cos γ & = \frac{\frac{1}{c}}{\sqrt[]{\frac{1}{a^{2}} + \frac{1}{b^{2}} + \frac{1}{c^{2}}}} . \end{matrix}

a rudakra ható erők pedig:

\begin{matrix} Q_{a} & = Q cos α = Q \frac{\frac{1}{a}}{\sqrt[]{\frac{1}{a^{2}} + \frac{1}{b^{2}} + \frac{1}{c^{2}}}}, \\ Q_{b} & = Q cos β = Q \frac{\frac{1}{b}}{\sqrt[]{\frac{1}{a^{2}} + \frac{1}{b^{2}} + \frac{1}{c^{2}}}}, \\ Q_{c} & = Q cos γ = Q \frac{\frac{1}{c}}{\sqrt[]{\frac{1}{a^{2}} + \frac{1}{b^{2}} + \frac{1}{c^{2}}}} . \end{matrix}

Abban az esetben, ha

a = b = c

, azaz a rudak egyenlő hosszúak,

\begin{matrix} Q_{a} = Q_{b} = Q_{c} = \frac{Q}{\sqrt[]{3}} . \end{matrix}