| Feladat: | 4211. fizika feladat | Korcsoport: 16-17 | Nehézségi fok: nehéz |
| Megoldó(k): | Balogh Péter , Werner Miklós Antal | ||
| Füzet: | 2010/május, 301 - 306. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Feladat, Hosszú egyenes vezető mágneses tere, Áramvezetőre ható erő, Hooke-törvény | ||
| Hivatkozás(ok): | Feladatok: 2009/december: 4211. fizika feladat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. megoldás. A cső tengelyében levő vezetékben és a cső falában folyó áram hatására mágneses mező alakul ki. Ez a mező a fémcső falában mozgó töltéshordozókra Lorentz-erőt fejt ki. Ez az erő növelni (vagy csökkenteni) igyekszik a fémcső sugarát; hatására a cső mérete megváltozik. A deformáció során a fémben rugalmas feszültségek alakulnak ki. A rendszer egyensúlyi állapotában a mágneses erők és a rugalmas erők éppen egyensúlyt tartanak. Mivel , feltételezhetjük, hogy a mágneses indukció egyenletesen (lineárisan) változik a cső sugara mentén, és a Lorentz-erőt számolhatjuk a külső és belső oldali mágneses indukciók 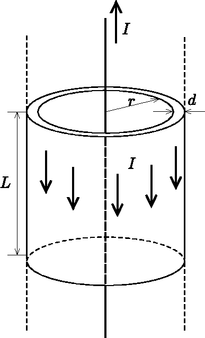 1. ábra Tekintsük a feladatban szereplő ,,végtelen hosszú'' elrendezésnek valamekkora hosszúságú részét (1. ábra), és vizsgáljuk ezen részben a fémcső egy kicsiny, a cső tengelyétől nézve szögben látszó darabkáját (2. ábra)! Ebben a darabkában a csőben folyó teljes áram arányos töredéke, tehát nagyságú áram folyik. Így ‐ az átlagos mágneses indukcióval számolva ‐ a csődarabkára
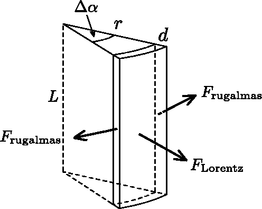 2. ábra Megjegyzés. Megmutatjuk, hogy az átlagos mágneses indukcióval való számolás akkor is helyes, ha a cső falában az árameloszlás nem homogén (de hengerszimmetrikus). 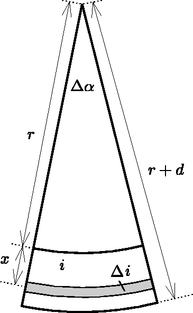 Daraboljuk fel a falvastagságú fémcsövet képzeletben sok, vékonyabb falú, közös tengelyű csőre, majd tekintsük ennek a (póréhagymára emlékeztető) csőseregnek egy szöggel jellemezhető szeletét (3. ábra)! Az egyes csövecskékben (rétegekben) folyjon áram, és egy adott réteg esetén jelöljük -vel azt az áramot, amely a tőle befelé eső csövecskékben összesen folyik. (A cső közepén levő vezetékben az erősségű áram az ábra síkjára merőlegesen felfelé, az áram pedig lefelé folyik.) Egy olyan rétegben, melynek a cső belső falától mért távolsága (nyilván ), vagyis a sugara , a mágneses indukció (a jobbkézszabálynak megfelelően) felülről nézve az óramutató járásával ellentétes irányba mutat, nagysága pedig: Válasszunk az 1. ábrán látható módon egy hosszúságú csődarabot, majd vegyük ennek (a 2. ábra szerint) egy nyílásszöghöz tartozó darabját. Célunk az, hogy kiszámítsuk az egyes rétegekre ható mágneses erőt, majd ezeket a teljes szélességre összegezve megkapjuk az hosszúságú, nyílásszögű csődarabkára ható eredő Lorentz-erőt. A hengerszimmetrikus árameloszlás miatt a vizsgált vezetőszálban nyilván nagyságú áram folyik. A jobbkézszabályt alkalmazva látjuk, hogy az erő sugár irányban kifelé fog mutatni, és a nagysága:
A (2) átalakítás eredménye geometriai úton, a 4. ábrán látható derékszögű háromszög területének kiszámításával, vagy az integrálszámítás formuláinak alkalmazásával is megkapható: 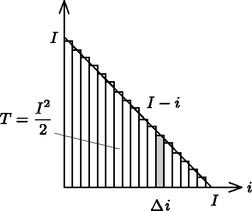 Az egyes csődarabkákra ható, sugár irányban kifelé mutató mágneses erő hatására a cső sugara az eredeti -ről valamekkora értékkel megnő. Ennek következtében a cső kerülete -ről -ra változik, a relatív megnyúlás tehát:
A rugalmas erők és a mágneses erők (lásd a 2. ábrát) akkor vannak egyensúlyban, ha fennáll a Megjegyzés. A megoldás során feltételeztük, hogy a relatív deformáció kicsiny, vagyis . Ha nem így lenne, a Hooke-törvény sem lenne érvényes, és a Young-modulus fogalma is használhatatlanná válna. A kicsiny sugárnövekedés miatt a mágneses Lorentz-erő számításánál a cső sugarát az eredeti, deformáció előtti értékével közelíthettük. 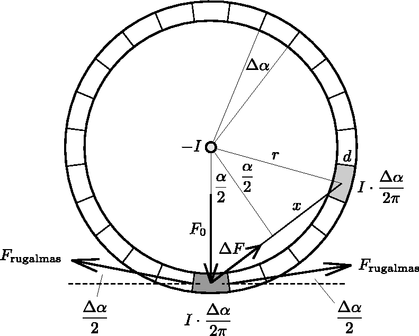 Ha a csövet részre osztjuk (), akkor az egyes csíkok szélei a tengelytől Másrészt a többi ,,csíkban'' folyó, a vizsgált darabkáéval megegyező irányú áramok is erőt fejtenek ki a kérdéses (sötétre színezett) csíkra. Ez az erő vonzóerő, amely a csövet igyekszik összehúzni. Az a ,,vezeték'', amelyik a vizsgált csíkhoz képest szögben elfordult helyzetben található, tehát távol van tőle, A cső relatív méretváltozása következtében a cső falában |