Kezdőlap


Feladat:	B.4210	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Ágoston Tamás , Csere Kálmán , Dolgos Tamás , Dudás Zsolt , Éles András , Hajdu Ákos , Hegedűs Csaba , Jernei Tamás , Karkus Zsuzsa , Kiss Melinda Flóra , Kószó Simon , Kovács Gábor , Márkus Bence , Máthé László , Mészáros András , Ódor Gergely , Perjési Gábor , Popper Dávid , Repka Dániel , Réti Dávid , Somogyi Ákos , Strenner Péter , Szabó Attila
Füzet:	2010/május, 278 - 279. oldal		PDF \| MathML
Témakör(ök):	Feladat, Szinusztétel alkalmazása, Egyenletek grafikus megoldása, Elsőfokú (lineáris) függvények, Trigonometrikus függvények
Hivatkozás(ok):	Feladatok: 2009/október: B.4210

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. Jelölje a háromszög szögeit a szokásos módon $α$ , $β$ és $γ$ . Szorozzuk meg az $a b c = a + b + c$ egyenlőséget $\frac{sin γ}{c}$ -vel és alkalmazzuk az $a b sin γ = 2 t$ összefüggést, valamint a szinusztételt:

\begin{matrix} 2 t = \frac{a b c sin γ}{c} = \frac{a sin γ}{c} + \frac{b sin γ}{c} + \frac{c sin γ}{c} = sin α + sin β + sin γ . \end{matrix}

Ezzel a bizonyítandó állítás

\begin{matrix} 2 < sin α + sin β + sin γ \leq \frac{3 \sqrt[]{3}}{2} . \end{matrix}

Mivel az

f (x) = sin x

függvény a

[0; \frac{π}{2}]

intervallumon alulról szigorúan konkáv, a Jensen-egyenlőtlenség szerint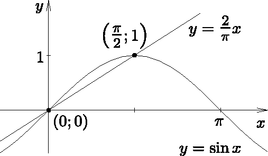

\begin{matrix} \frac{sin α + sin β + sin γ}{3} \leq sin \frac{α + β + γ}{3} = sin 60^{\circ} = \frac{\sqrt[]{3}}{2}, \end{matrix}

ahol egyenlőség csakis az

α = β = γ = 60^{\circ}

esetben áll fenn. Ezzel a felső becslést beláttuk.

Az alsó becslés bizonyításához szintén a szinuszfüggvény konkávságát használjuk. Ebből ugyanis következik, hogy a

(0; 0)

pontot a

(\frac{π}{2}; 1)

ponttal összekötő

y = \frac{2}{π} x

egyenletű egyenes a függvénygörbe alatt halad. Ezért

\begin{matrix} \frac{2}{π} α < sin α, \frac{2}{π} β < sin β és \frac{2}{π} γ < sin γ . \end{matrix}

Ezeket összeadva kapjuk, hogy

\begin{matrix} \frac{2}{π} (α + β + γ) < sin α + + sin β + sin γ . \end{matrix}

Ebből viszont

α + β + γ = π

miatt rögtön adódik a bizonyítandó

2 < sin α + sin β + sin γ

egyenlőtlenség. Az is látszik, hogy egyenlőség nem állhat fenn, és a becslés nem javítható, mert a szögek szinuszainak az összege tetszőlegesen közel lehet

2

-höz például azokban az egyenlőszárú háromszögekben, melyeknek alapon fekvő szögei majdnem derékszögek.