Kezdőlap


Feladat:	4223. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Csopor Dávid , Galzó Ákos Ferenc , Hartstein Máté , Jéhn Zoltán , Patartics Bálint
Füzet:	2010/április, 246 - 249. oldal		PDF \| MathML
Témakör(ök):	Feladat, Egyéb magfizika, Egyéb ütközések
Hivatkozás(ok):	Feladatok: 2010/január: 4223. fizika feladat

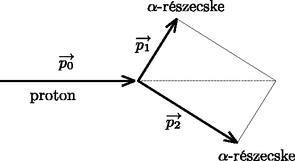
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jelöljük a proton lendületvektorát $\vec{p_{0}}$ -lal, a keletkező $α$ -részecskék lendületét pedig $\vec{p_{1}}$ és $\vec{p_{2}}$ vektorokkal! A folyamat során a lendület megmarad:

\begin{matrix} \vec{p_{0}} = \vec{p_{1}} + \vec{p_{2}} . \end{matrix}

Igaz továbbá, hogy ha a keletkező részecskék derékszögben repülnek szét (lásd az ábrát), akkor Pitagorasz tétele szerint

\begin{matrix} p_{1}^{2} + p_{2}^{2} = p_{0}^{2} . \end{matrix}

(1)

(A fenti képletben a nyilazás nélküli kifejezések a megfelelő vektorok hosszát jelölik.)

A folyamat során az energia is megmaradó mennyiség. Ha a reakcióban részt vevő részecskék sebessége a fénysebességhez képest elhanyagolhatóan kicsiny volna, akkor a newtoni fizika képleteit, nevezetesen a

\begin{matrix} p = m v és E = \frac{1}{2} m v^{2} = \frac{p^{2}}{2 m} \end{matrix}

összefüggéseket alkalmazhatnánk. Ezekkel felírva az energiamegmaradás törvényét:

\begin{matrix} \frac{p_{0}^{2}}{2 m_{p}} = \frac{p_{1}^{2}}{2 m_{α}} + \frac{p_{2}^{2}}{2 m_{α}} . \end{matrix}

(2)

Mivel az

α

-részecskék

m_{α}

tömege jó közelítéssel az

m_{p}

porotontömeg négyszerese, (2) így írható:

\begin{matrix} p_{1}^{2} + p_{2}^{2} = 4 p_{0}^{2}, \end{matrix}

(3)

ami nyilvánvalóan ellentmond (1)-nek! A részecskék mozgása tehát nem írható le a newtoni fizika törvényeivel, feltétlenül szükséges a relativisztikus tárgyalás.
Egy

m

(nyugalmi) tömegű,

v

sebességű részecske relativisztikus impulzusát a

\begin{matrix} p = \frac{m v}{\sqrt[]{1 - v^{2} / c^{2}}}, \end{matrix}

(4)

energiáját pedig az

\begin{matrix} E = \frac{m c^{2}}{\sqrt[]{1 - v^{2} / c^{2}}} \end{matrix}

(5)

összefüggések adják meg (

c

a vákuumbeli fénysebesség). (4)-ből és (5)-ből a sebesség kiküszöbölése után az energia és az impulzus között az

\begin{matrix} E = \sqrt[]{p^{2} c^{2} + m^{2} c^{4}} \end{matrix}

(6)

relációt kapjuk.
A vizsgált folyamat relativisztikus energia-tétele

\begin{matrix} \sqrt[]{p_{0}^{2} c^{2} + m_{p}^{2} c^{4}} + m_{Li} c^{2} = \sqrt[]{p_{1}^{2} c^{2} + m_{α}^{2} c^{4}} + \sqrt[]{p_{2}^{2} c^{2} + m_{α}^{2} c^{4}}, \end{matrix}

ami a jó közelítéssel érvényes

m_{Li} = 7 m_{p}

és

m_{α} = 4 m_{p}

miatt így is felírható:

\begin{matrix} \sqrt[]{{(\frac{p_{0}}{m_{p} c})}^{2} + 1} + 7 = \sqrt[]{{(\frac{p_{1}}{m_{p} c})}^{2} + 16} + \sqrt[]{{(\frac{p_{2}}{m_{p} c})}^{2} + 16.} \end{matrix}

Érdemes bevezetni az

\begin{matrix} x = \frac{p_{1}}{m_{p} c}, y = \frac{p_{2}}{m_{p} c} és z = \frac{p_{0}}{m_{p} c} \end{matrix}

dimenziótlan új változókat, melyek között (1) miatt fennáll az

\begin{matrix} x^{2} + y^{2} = z^{2} \end{matrix}

(7)

összefüggés. Az energiamegmaradás egyenlete az új változókkal kifejezve:

\begin{matrix} \sqrt[]{z^{2} + 1} + 7 = \sqrt[]{x^{2} + 16} + \sqrt[]{y^{2} + 16} . \end{matrix}

(8)

Feladatunk

z

azon legkisebb értékének meghatározása, amely kielégíti a (8) egyenletet és (7) mellékfeltételt. A (7) összefüggés felhasználásával (8) így is írható:

\begin{matrix} \sqrt[]{z^{2} + 1} + 7 = \sqrt[]{x^{2} + 16} + \sqrt[]{z^{2} - x^{2} + 16} . \end{matrix}

(9)

Deriváljuk (9) mindkét oldalát

x

szerint, és használjuk ki, hogy a szélsőérték helyén

\frac{d z}{d x} = 0

\begin{matrix} 0 = \frac{x}{\sqrt[]{x^{2} + 16}} - \frac{x}{\sqrt[]{z^{2} - x^{2} + 16}} . \end{matrix}

Ebből rendezve

\begin{matrix} x = \frac{z}{\sqrt[]{2}}, y = \frac{z}{\sqrt[]{2}}, \end{matrix}

(10)

vagyis a

\begin{matrix} p_{1} = p_{2} = \frac{p_{0}}{\sqrt[]{2}} \end{matrix}

eredmény adódik. A keresett határesetben tehát a két

α

-részecske egyforma nagyságú impulzussal, a beérkező proton mozgásirányához képest szimmetrikusan,

45^{\circ}

-os szögben repül szét. Visszahelyettesítve a (10)-ben szereplő értékeket (8)-ba és azt

z > 0

-ra megoldva

z = \sqrt[]{168}

, vagyis a proton minimális impulzusára a

\begin{matrix} p_{min} = \sqrt[]{168} \cdot m_{p} c \end{matrix}

eredmény adódik. Ezt (4)-gyel összevetve a proton sebességére a

\begin{matrix} \frac{v}{c} \geq \sqrt[]{\frac{168}{169}} = 0, 997 \end{matrix}

korlátot kapjuk. (Ekkora a sebességgel a legalább 12 GeV energiára felgyorsított protonok rendelkeznek.)

II. megoldás. Jelölje a részecskék tömegét, energiáját, impulzusát rendre

m_{i}

E_{i}

és

p_{i}

, ahol az

i

index helyére p,

α

, vagy Li írandó aszerint, hogy protonról, alfa-részecskéről vagy Li-atommagról van szó. Az egyszerűség kedvéért használjunk olyan egységrendszert, amelyben a

c

fénysebesség egységnyi nagyságú.¹
A részecskék energiája és impulzusa között minden pillanatban fennáll az

E_{i}^{2} = p_{i}^{2} + m_{i}^{2}

egyenlőség (a relativitáselméletben ezt tömeghéj-feltételnek nevezik). Az ütközésre érvényes az energiamegmaradás:

\begin{matrix} E_{p} + E_{Li} = E_{α,1} + E_{α,2}, \end{matrix}

amely a tömeghéj-feltétellel így írható:

\begin{matrix} \sqrt[]{p_{p}^{2} + m_{p}^{2}} + m_{Li} = \sqrt[]{p_{α,1}^{2} + m_{α}^{2}} + \sqrt[]{p_{α,2}^{2} + m_{α}^{2}} . \end{matrix}

(1)

Másrészt (mivel a részecskerendszerre külső erő nem hat) teljesül az impulzusmegmaradás is:

\begin{matrix} p_{p} = p_{α,1} + p_{α,2}, \end{matrix}

amiből a

90^{\circ}

-ban szétrepülő

α

-részecskék miatt (Pitagorasz tétele szerint)

\begin{matrix} p_{p}^{2} = p_{α,1}^{2} + p_{α,2}^{2} \end{matrix}

(2)

következik.
Az (1) egyenlet jobb oldala a számtani és négyzetes közepek közötti egyenlőtlenség segítségével átírható a következőképpen:

\begin{matrix} \frac{\sqrt[]{p_{α,1}^{2} + m_{α}^{2}} + \sqrt[]{p_{α,2}^{2} + m_{α}^{2}}}{2} \leq \sqrt[]{\frac{p_{α,1}^{2} + m_{α}^{2} + p_{α,2}^{2} + m_{α}^{2}}{2}}, \end{matrix}

ami (2) felhasználásával

\begin{matrix} \sqrt[]{p_{α,1}^{2} + m_{α}^{2}} + \sqrt[]{p_{α,2}^{2} + m_{α}^{2}} \leq \sqrt[]{2 (p_{p}^{2} + 2 m_{α}^{2})} \end{matrix}

alakra hozható. Ezt az (1) energia-mérlegegyenlettel összevetve egy olyan egyenlőtlenséghez jutunk, amiben már csak

p_{p}^{2}

a változó:

\begin{matrix} \sqrt[]{p_{p}^{2} + m_{p}^{2}} + m_{Li} \leq \sqrt[]{2 (p_{p}^{2} + 2 m_{α}^{2})} . \end{matrix}

(3)

Négyzetre emelés, majd rendezés után (3)-ból a következőhöz jutunk:

\begin{matrix} 0 \leq p_{p}^{4} - 2 p_{p}^{2} (m_{p}^{2} + 3 m_{Li}^{2} - 4 m_{α}^{2}) + [{(4 m_{α}^{2} - m_{p}^{2} - m_{Li}^{2})}^{2} - 4 m_{p}^{2} m_{Li}^{2}] . \end{matrix}

(4)

p_{p}^{2}

-re nézve másodfokú egyenlőtlenség.
Ha a magok kötési energiáját elhanyagoljuk, vagyis az

\begin{matrix} m_{Li} \approx 7 m_{p}, m_{α} \approx 4 m_{p} \end{matrix}

(5)

közelítéseket használjuk, (4) jobb oldalán a szögletes zárójelben álló konstans tag értéke nullának adódik. Táblázatbeli, pontos tömegértékek felhasználásával persze erre a kifejezésre véges értéket kapunk, de mivel (a feladat szövege szerint) a proton nagy energiájú (ezért nagy impulzusú is), így (4) jobb oldalán az első két tag mellett az utolsót nyugodtan elhanyagolhatjuk.
Mivel

p_{p}^{2}

értéke biztosan nagyobb, mint nulla, a (4) egyenlőtlenségből a következőt kapjuk:

\begin{matrix} | p_{p} | \geq \sqrt[]{2 m_{p}^{2} + 6 m_{Li}^{2} - 8 m_{α}^{2}} . \end{matrix}

Az (5) közelítésekkel és a fénysebesség visszaírásával a proton impulzusára a

\begin{matrix} | p_{p} | \geq \sqrt[]{168} m_{p} c \end{matrix}

megszorítást kapjuk. A relativisztikus impulzus

\begin{matrix} | p_{p} | = \frac{m_{p} v}{\sqrt[]{1 - v^{2} / c^{2}}} \end{matrix}

kifejezését felhasználva ez azt jelenti, hogy a proton sebessége az ütközés előtt

\begin{matrix} v = 0, 997 c, \end{matrix}

vagyis a fénysebesség 99,7 százaléka volt.
(Vígh Máté)

¹A

c = 1

választás áttekinthetőbbé teszi a megoldást, a hiányzó

c

-ket pedig a számolás végén a dimenzióanalízis módszerének alkalmazásával egyszerűen visszaírhatjuk.