Kezdőlap


Feladat:	2009. évi Eötvös fizikaverseny 1. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Füzet:	2010/március, 165 - 168. oldal		PDF \| MathML
Témakör(ök):	Eötvös Loránd (korábban Károly Irén), Gördülés (Merev testek síkmozgása)
Hivatkozás(ok):	Feladatok: 2010/március: 2009. évi Eötvös fizikaverseny 1. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. $a)$ A megoldást érdemes az egyenletesen gyorsuló gömb esetével kezdenünk (hiszen ez speciális esetként tartalmazza az egyenletesen forgó és az álló gömb esetét is).
Tegyük fel, hogy a gömb $P$ pontja $φ$ szöggel fordul el a kiindulási, legalsó helyzetből (1. ábra). Eközben a golyó tiszta gördüléssel mozog, és a golyó $C$ középpontja $ϑ$ szöggel fordul el. A golyónak a gömb egyes felületi pontjaihoz képesti összes elfordulása:

\begin{matrix} \frac{R (φ - ϑ)}{r} . \end{matrix}

A golyó teljes

ψ

elfordulását úgy kaphatjuk meg, ha a gömb felszínéhez képesti elforduláshoz hozzáadjuk még a golyó

C

középpontjának elfordulását is:

\begin{matrix} ψ = \frac{R (φ - ϑ)}{r} + ϑ = \frac{R}{r} φ - \frac{R - r}{r} ϑ . \end{matrix}

(1)

1. ábra

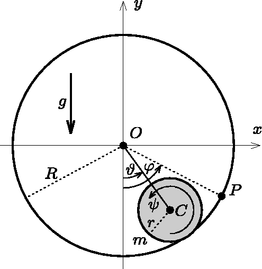Jelöljük a plexigömb (állandó) szöggyorsulását

β

-val, a golyó tömegközéppontjának érintő irányú gyorsulás-összetevőjét

a

-val, a golyó saját középpontja körüli szöggyorsulását pedig

β_{golyó}

-val. Mivel a szögelfordulások és a szöggyorsulások (egy bizonyos rövid időtartam alatt) arányosak egymással, az (1) összefüggésből leolvasható a szöggyorsulásokra vonatkozó megszorítás, tehát a mozgás kényszerfeltétele is:

\begin{matrix} β_{golyó} = \frac{R}{r} β - \frac{R - r}{r} \cdot \frac{a}{R - r} . \end{matrix}

(2)

Megjegyzés: (2)-t átrendezve

R β = a + r β_{golyó}

alakra hozhatjuk, ami azt fejezi ki, hogy a gömb felszínének érintőleges gyorsulása a golyó tömegközépponti és kerületi gyorsulásának összege. Kényszerfeltételek felírásában gyakorlottak ezt a kapcsolatot számolás nélkül, ránézésre is fel tudják írni.

A golyóra ható súrlódási erőt jelöljük

S

-sel, a golyó tömegközéppontjának szöggyorsulását pedig

β_{t}

-vel! Ez utóbbi nyilván kifejezhető a tömegközéppont érintőleges gyorsulásával:

\begin{matrix} β_{t} = \frac{a}{R - r} . \end{matrix}

(3)

A dinamikai egyenletek:

\begin{matrix} S - m g sin ϑ = m a = m (R - r) β_{t}, & (4) \\ S r = \frac{2}{5} m r^{2} β_{golyó} . & (5) \end{matrix}

A (2)‐(5) egyenletrendszerből kiküszöbölve az

S

a

és

β_{golyó}

mennyiségeket, a golyó tömegközéppontjának szögkitérése és szöggyorsulása között a következő összefüggést kapjuk:

\begin{matrix} β_{t} = - \frac{5 g}{7 (R - r)} (sin ϑ - \frac{2 R β}{5 g}) . \end{matrix}

(6)

Innen leolvashatjuk, hogy általában létezik egy olyan

\begin{matrix} ϑ_{0} = arcsin \frac{2 R β}{5 g} \end{matrix}

szög, amelynek megfelelő helyzetben a golyó tömegközéppontja egyensúlyban van.

Megjegyzés: Ha ebből a helyzetből indítjuk a golyót, akkor a tömegközéppontja nyugalomban marad, a tömegközéppont körüli forgásának szögsebessége pedig (a csúszásmentes gördülés feltételének megfelelően)

\begin{matrix} ω_{golyó} = \frac{R}{r} \cdot β t \end{matrix}

módon növekszik. Ehhez a megfelelően nagy súrlódáson kívül a szöggyorsulás se lehet akármilyen nagy.

Mivel a feladat szövegében az szerepel, hogy a

β

szöggyorsulás értéke kicsi, ezért jogos feltennünk, hogy a golyó tömegközéppontjának maximális elmozdulása is kicsi, vagyis indokolt a

sin ϑ \approx ϑ

közelítés használata. A (6) mozgásegyenlet ebben a közelítésben a

\begin{matrix} β_{t} = - \frac{5 g}{7 (R - r)} (ϑ - \frac{2 R β}{5 g}) = - Ω^{2} \cdot (ϑ - ϑ_{0}) \end{matrix}

alakú, amelyből látszik, hogy a golyó tömegközéppontja jó közelítéssel harmonikus rezgőmozgást végez a

ϑ_{0}

szöghelyzet körül, és a rezgésideje:

\begin{matrix} T = \frac{2 π}{Ω} = 2 π \sqrt[]{\frac{7 (R - r)}{5 g}} . \end{matrix}

(7)

A rezgőmozgás szög-amplitúdója (mivel

ϑ = 0

helyzetből indult a golyó) jó közelítéssel

ϑ_{0}

. Meglepő, hogy a rezgésidő akkor is a (7)-nek megfelelő érték, ha a gömb szöggyorsulása nulla, a gömb egyenletesen forog vagy áll, vagyis

a)

mindhárom kérdésére ugyanaz a válasz.

b)

Legyen a plexigömb kezdeti állandó szögsebessége

ω_{gömb}

. A tiszta gördülés miatt a gumigolyó ugyanabba az irányba forog, és a golyó szögsebessége:

\begin{matrix} ω_{golyó} = \frac{R}{r} ω_{gömb} . \end{matrix}

(Ezt pl. (1)-ből olvashatjuk le,

ϑ \equiv 0

helyettesítéssel.)
A plexigömb megállításának pillanatában változó nagyságú

F_{s} (t)

súrlódási erő kezd hatni a golyóra, ami valamekkora

Δ t

idő alatt tiszta gördülést eredményez. A súrlódási erő (melynek átlagértékét jelöljük

\bar{F}

-sal) a golyó tömegközéppontjának valamekkora

v_{0}

sebességet ad, míg a golyó szögsebességét

ω_{0}

értékre csökkenti. A tiszta gördülési feltétel miatt:

v_{0} = r ω_{0}

.
Írjuk fel a súrlódási erő sebességet, illetve szögsebességet változtató hatását kifejező dinamikai egyenleteket:

\begin{matrix} \bar{F} Δ t = m v_{0} = m r ω_{0}, \\ r \bar{F} Δ t = Θ \cdot Δ ω = \frac{2}{5} m r^{2} \cdot (ω_{golyó} - ω_{0}) = \frac{2}{5} m r^{2} \cdot (\frac{R}{r} ω_{gömb} - ω_{0}) . \end{matrix}

A fenti egyenletekből

\bar{F} Δ t

-t kiküszöbölve a tisztán gördülő golyó adataira

\begin{matrix} ω_{0} = \frac{2 R}{7 r} ω_{gömb} és v_{0} = \frac{2 R}{7} ω_{gömb} \end{matrix}

(8)

adódik. Mivel ez az állapot (a plexigömb érdes felülete miatt) a gömb megállítása után igen rövid idővel bekövetkezik, feltehetjük, hogy az újra tiszta gördüléssel mozgó golyó lényegében a gömb legalján marad, elmozdulása a megcsúszás közben elhanyagolható.

Megjegyzés: Ugyanerre az eredményre juthatunk akkor is, ha a gömb megállítását követő rövid időre a golyó alatti felületet vízszintes, igen érdes síknak tekintjük. A rövid ideig ható súrlódási ,,erőlökés'' megváltoztatja a golyó mechanikai energiáját és lendületét, de nem változtatja meg a golyónak a gömbbel érintkező pontjára vonatkoztatott perdületét:

\begin{matrix} \frac{2}{5} m r^{2} \cdot ω_{golyó} = \frac{2}{5} m r^{2} \cdot ω_{0} + m v_{0} \cdot r . \end{matrix}

Ez a feltétel

v_{0} = r ω_{0}

és

r ω_{golyó} = R ω_{gömb}

miatt (8)-cal egyenértékű.

A golyó további (tisztán gördülő) mozgása során felhasználhatjuk az energiamegmaradás törvényét, és felírjuk a tömegközéppontra vonatkozó mozgásegyenletet a golyó pályájának bármelyik, például a legfelső pontjára is:

\begin{matrix} m g - K = m \frac{v_{1}^{2}}{R - r}, \\ \frac{1}{2} m v_{0}^{2} + \frac{1}{2} Θ ω_{0}^{2} = m g \cdot 2 (R - r) + \frac{1}{2} m v_{1}^{2} + \frac{1}{2} Θ ω_{1}^{2}, \end{matrix}

ahol

v_{1}

és

ω_{1}

a golyó sebessége, illetve szögsebessége a pálya legfelső pontjában (

v_{1} = r ω_{1}

K

pedig a golyó és a plexigömb között fellépő nyomóerőt jelöli ebben a helyzetben.
A megfelelő mennyiségek behelyettesítése után a kényszererőt így fejezhetjük ki a plexigömb kezdeti szögsebességével:

\begin{matrix} K = \frac{4}{49} \frac{m R^{2} ω_{gömb}^{2}}{R - r} - \frac{27}{7} m g . \end{matrix}

A gumigolyó akkor juthat fel a legfelső pontba, ha a

K

kényszererő még a pálya legfelső pontjában sem negatív

(K \geq 0)

, ami a következő feltételt adja a gömb kezdeti szögsebességére:

\begin{matrix} ω_{gömb} \geq \frac{3}{2 R} \sqrt[]{21 (R - r) g} . \end{matrix}