Kezdőlap


Feladat:	B.4194	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Dudás Zsolt , Strenner Péter
Füzet:	2010/március, 149 - 150. oldal		PDF \| MathML
Témakör(ök):	Feladat, Középponti és kerületi szögek, Pitagorasz-tétel alkalmazásai, Thalesz tétel és megfordítása, Szögfelező egyenes, Síkgeometriai számítások trigonometriával
Hivatkozás(ok):	Feladatok: 2009/szeptember: B.4194

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen a $b$ befogó $C$ -től különböző végpontja $A$ , a háromszög harmadik csúcsa pedig $B$ . Ekkor Thalész tételének megfordításából következik, hogy $A B$ a körülírt $k$ kör átmérője. Egy kör középpontjából a kör tetszőleges húrjára állított merőleges felezi a húrt, ezért $C E$ és $A B$ merőlegességéből következik, hogy $C$ és $E$ az $A B$ -re szimmetrikusan helyezkedik el, tehát $C A B ∢ = E A B ∢ = α$ . Mivel $b$ a nem kisebb befogó, azért $α \leq 45^{\circ}$ . A $C D$ szakasz szögfelező, így $A C D ∢ = B C D ∢ = 45^{\circ}$ , a kerületi szögek tétele szerint pedig 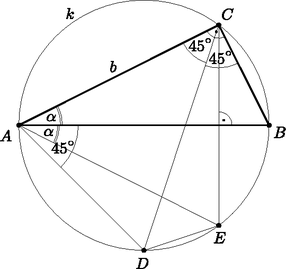$B A D ∢ = B C D ∢ = 45^{\circ}$ . Tehát

\begin{matrix} D A C ∢ = B A D ∢ + B A C ∢ = 45^{\circ} + α, \end{matrix}

továbbá

\begin{matrix} E A D ∢ = B A D ∢ - B A E ∢ = 45^{\circ} - α . \end{matrix}

A B

átmérőjű

k

kör nemcsak az

A B C

, hanem az

A D C

és az

A E D

háromszögeknek is köréírt köre, ezért az általánosított szinusztétel szerint

\begin{matrix} C D = A B sin (45^{\circ} + α) és D E = A B sin (45^{\circ} - α) . \end{matrix}

Tehát

\begin{matrix} C D + D E & = A B (sin (45^{\circ} + α) + sin (45^{\circ} - α)) = \\ = 2 A B sin 45^{\circ} cos α = A B \sqrt[]{2} cos α = b \sqrt[]{2} . \end{matrix}

Ezzel az állítást beláttuk.

II. megoldás. Használjuk az I. megoldás jelöléseit, legyen továbbá

B C = a

, a háromszög

C

-hez tartozó magasságának hossza pedig

m

. Ekkor Pithagorasz tétele szerint

A B = \sqrt[]{a^{2} + b^{2}}

és

m = a b / \sqrt[]{a^{2} + b^{2}}

, hiszen az

A B C

háromszög területének kétszeresével egyezik meg az

a b

és az

m \sqrt[]{a^{2} + b^{2}}

szorzat is.

Az I. megoldásban láttuk, hogy

E

-nek az

A B

-re vonatkozó tükörképe

C

. Mivel

C D

szögfelező,

D

felezi az

A B

ívet. Tehát ha

D

-nek az

A B

-re vonatkozó tükörképe

F

, akkor

D F

is átmérője

k

-nak, a

D F C E

négyszög pedig (esetleg elfajuló) szimmetrikus trapéz. Ezért

D E = C F

. Ha a

C

-ből

D F

-re bocsájtott merőleges talppontja

T

, akkor

\begin{matrix} T F = (D F - E C) / 2 és D T = D F - T F = (D F + E C) / 2. \end{matrix}

Thalész tétele szerint

D C F ∢ = 90^{\circ}

. A

C D F

derékszögű háromszög átfogója

D F = A B = \sqrt[]{a^{2} + b^{2}}

, a befogótétel szerint tehát

\begin{matrix} C D & = \sqrt[]{D F \cdot D T} = \sqrt[]{\sqrt[]{a^{2} + b^{2}} \cdot (\frac{\sqrt[]{a^{2} + b^{2}}}{2} + \frac{a b}{\sqrt[]{a^{2} + b^{2}}})} = \\ = \sqrt[]{\frac{a^{2} + b^{2}}{2} + a b} = \sqrt[]{\frac{{(a + b)}^{2}}{2}} = \frac{a + b}{\sqrt[]{2}}, \end{matrix}

és (felhasználva, hogy

b \geq a

, azaz

b - a \geq 0

)

\begin{matrix} C F & = \sqrt[]{D F \cdot T F} = \sqrt[]{\sqrt[]{a^{2} + b^{2}} \cdot (\frac{\sqrt[]{a^{2} + b^{2}}}{2} - \frac{a b}{\sqrt[]{a^{2} + b^{2}}})} = \\ = \sqrt[]{\frac{a^{2} + b^{2}}{2} - a b} = \sqrt[]{\frac{{(b - a)}^{2}}{2}} = \frac{b - a}{\sqrt[]{2}} . \end{matrix}

Tehát

\begin{matrix} C D + D E = C D + C F = \frac{a + b}{\sqrt[]{2}} + \frac{b - a}{\sqrt[]{2}} = b \sqrt[]{2}, \end{matrix}

ami épp a bizonyítandó állítás.