Kezdőlap


Feladat:	4170. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Zsakó András
Füzet:	2010/január, 53 - 54. oldal		PDF \| MathML
Témakör(ök):	Feladat, Egyéb ellenállás-kapcsolások
Hivatkozás(ok):	Feladatok: 2009/május: 4170. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. Jelöljük az első ,,lépcső'' csúcsait az 1. ábrán látható módon! Az $A$ és $B$ pontok közötti eredő ellenállást úgy mérhetjük meg, hogy az $A$ pontnál bevezetünk valamekkora, mondjuk 1 A erősségű áramot, a $B$ pontnál ugyanekkora áramot elvezetünk. Ha megmérjük az $A$ és $B$ pont közötti feszültséget, annak számértéke éppen az eredő ellenállással lesz egyenlő.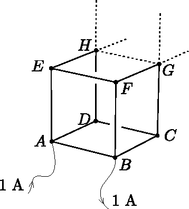

1. ábra

Vegyük észre, hogy az említett kapcsolásban ‐ a rács szimmetriája miatt ‐ a

C

és

F

pontok ekvipotenciálisak, és ugyancsak azonos potenciálú a

D

és az

E

pont is. Ezért a ,,lépcső'' ellenállása nem változna meg, ha ezeket a csúcspont-párokat összekötnénk. Jelöljük

C / F

-fel és

D / E

-vel ezeket a rövidrezárt pontokat!
Másik észrevételünk: a nagyon hosszú lépcsőnek

G

és

H

közötti (az ábrán szaggatott vonallal jelölt) részének eredő ellenállása ugyanakkora, mint az

A

és

B

pont közötti eredő ellenállás. Jelöljük ezt a (keresett) eredő ellenállást

r

-rel! A kapcsolás a 2. ábrán látható módon átrajzolható, és az eredő ellenállása soros és párhuzamos kapcsolások sorozataként számítható.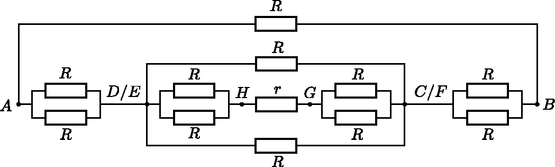

2. ábra

Az egymással párhuzamosan kapcsolt

R

nagyságú ellenállások egy-egy

R / 2

nagyságú ellenállással helyettesíthetők. A

D / E

és

C / F

pontok között három párhuzamos ágat látunk. Ezek eredője

\begin{matrix} {(\frac{1}{R} + \frac{1}{r + R} + \frac{1}{R})}^{- 1} = \frac{R (r + R)}{2 r + 3 R}, \end{matrix}

A

és

B

pontok közötti alsó ág teljes ellenállása pedig

\begin{matrix} \frac{R}{2} + \frac{R (r + R)}{2 r + 3 R} + \frac{R}{2} = \frac{R (3 r + 4 R)}{2 r + 3 R} . \end{matrix}

Ezzel az ellenállással párhuzamosan van kapcsolva a felső ág

R

ellenállása, és az eredőjük (a lépcső ,,végtelen'' hosszúságából adódó feltétel szerint)

r

kell legyen:

\begin{matrix} \frac{1}{R} + \frac{2 r + 3 R}{R (3 r + 4 R)} = \frac{1}{r} . \end{matrix}

Ez a feltétel algebrai átalakítások után

\begin{matrix} 5 r^{2} + 4 R r - 4 R^{2} = 0 \end{matrix}

alakra hozható. Ennek a másodfokú egyenletnek pozitív megoldása

r

-re:

\begin{matrix} r = \frac{2}{5} (\sqrt[]{6} - 1) \cdot R \approx 0, 58 R . \end{matrix}