Kezdőlap


Feladat:	B.4182	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Loose Lilla
Füzet:	2009/december, 537. oldal		PDF \| MathML
Témakör(ök):	Feladat, Ellipszis, mint mértani hely, Számtani közép, Mértani közép, Terület, felszín
Hivatkozás(ok):	Feladatok: 2009/május: B.4182

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. Legyen az ellipszis nagytengelyének hossza $2 a$ , kistengelyének hossza $2 b$ $(a > b)$ , az $F_{1}$ és $F_{2}$ fókuszpontjainak távolsága pedig $2 c$ . Tudjuk, hogy ekkor $a^{2} = b^{2} + c^{2}$ . A $t$ területű derékszögű háromszög fókuszoktól különböző csúcsa legyen $P$ , befogóinak hossza pedig $d$ és $e$ . A $P$ az $F_{1} F_{2}$ szakasz Thalész körének és az ellipszisnek a metszéspontja, ezért pontosan akkor létezik a feltételeknek megfelelő háromszög, ha 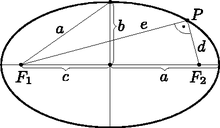$c \geq b$ .

P F_{1} F_{2}

háromszög területe

\begin{matrix} t = \frac{d e}{2}, \end{matrix}

az ellipszis területe pedig

a b π

. Az ellipszis definíciójából következik, hogy

\begin{matrix} d + e = 2 a, azaz d^{2} + e^{2} + 2 d e = 4 a^{2}, vagyis 4 t = 4 a^{2} - d^{2} - e^{2} . \end{matrix}

Pitagorasz tételét és az ellipszis tengelyeinek hossza, valamint fókuszainak távolsága közti összefüggést felhasználva kapjuk, hogy

\begin{matrix} d^{2} + e^{2} = {(2 c)}^{2} = 4 c^{2} = 4 a^{2} - 4 b^{2} . \end{matrix}

Tehát

\begin{matrix} 4 t = 4 a^{2} - (4 a^{2} - 4 b^{2}) = 4 b^{2}, azaz t = b^{2} . \end{matrix}

Vagyis azt kell bizonyítanunk, hogy

\begin{matrix} a b π \geq \sqrt[]{2} b^{2} π, azaz a \geq \sqrt[]{2} b . \end{matrix}

Ez viszont teljesül, mert

c \geq b

miatt

\begin{matrix} a^{2} = b^{2} + c^{2} \geq 2 b^{2} . \end{matrix}

Tehát ha létezik a feltételeknek eleget tevő háromszög, akkor az ellipszis területe legalább

\sqrt[]{2} π t

. Egyenlőség pontosan akkor van, ha az ellipszis fókuszainak távolsága megegyezik kistengelyének hosszával, a háromszög harmadik csúcsa pedig a kistengely valamelyik végpontja.