Kezdőlap


Feladat:	B.4132	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Ágoston Tamás , Blázsik Zoltán , Bodor Bertalan , Éles András , Énekes Péter , Fonyó Dávid , Kalina Kende , Kiss Melinda Flóra , Lovas Lia Izabella , Márkus Bence , Mester Márton , Nagy Donát , Nagy Róbert , Perjési Gábor , Strenner Péter , Szenczi Zoltán , Varga László , Viharos Andor , Weisz Ágoston
Füzet:	2009/december, 530 - 532. oldal		PDF \| MathML
Témakör(ök):	Oszthatóság, Többszemélyes véges játékok, Feladat
Hivatkozás(ok):	Feladatok: 2008/december: B.4132

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. A kérdésre adandó válasz attól függ, hogy a sakktábla oldalhossza, amit a továbbiakban $n$ -nel jelölünk, 3-mal osztva mennyi maradékot ad.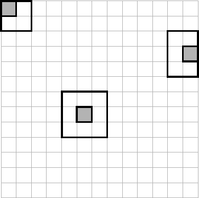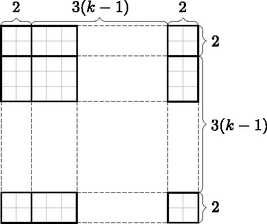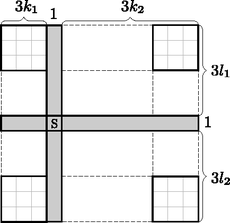
Egy pozitív egész számot nevezzünk szépnek, ha 3-mal osztva 1 maradékot ad. Az $n \times n$ -es sakktábla sorait és oszlopait is számozzuk meg sorban 1-től $n$ -ig, és egy sort, illetve oszlopot nevezzünk szépnek akkor, ha sorszáma szép. Egy mező legyen szép, ha sor- és oszlopindexe is szép, átlagos, ha sor- és oszlopindexe közül pontosan az egyik szép, egyébként pedig csúnya.
Tegyük fel, hogy $n = 3 k + 2$ alakú, ahol $k \geq 0$ egész. Ha Aranka éppen a szép mezőket választja ki, akkor minden mezőre 1-et ír, akárcsak abban az esetben, ha azokat a mezőket választja ki, amelyeknek sor- és oszlopindexe is 2 maradékot ad 3-mal osztva. Ezért ha $(3 k + 2) \times (3 k + 2)$ -es (speciálisan $2009 \times 2009$ -es) táblán játszanak, akkor van olyan eset, amikor Bianka nem tudja meghatározni az Aranka által kiválasztott mezőket.
Megmutatjuk, hogy ha viszont $n$ szép, akkor $n \times n$ -es (speciálisan $2008 \times 2008$ -as) tábla esetén Bianka mindig egyértelműen meg tudja mondani, hogy mely mezőket választotta ki Aranka. A sakktábla egy részét nevezzük kiszámolhatónak, ha Bianka ki tudja számolni, hogy az adott rész összesen hány kiválasztott mezőt tartalmaz. Azt kell megmutatnunk, hogy a sakktábla egyetlen mezőből álló részei mind kiszámolhatók.
Nevezzük elemi téglalapnak a sakktábla $3 \times 3$ -as résztábláit, a vízszintes szélek mentén található $2 \times 3$ -as, illetve a függőleges szélek mentén található $3 \times 2$ -es résztáblákat, valamint a sarkokban elhelyezkedő $2 \times 2$ -es résztáblákat. Az 1. ábrán látható, hogy minden elemi téglalapnak van egy ,,közepe'', amelyre írt szám megegyezik azoknak a mezőknek a számával, amelyeket Aranka a szóban forgó elemi téglalapból kiválasztott. (Minden elemi téglalapban a ,,közép'' az egyetlen olyan mező, amelyre írt szám értéke csak az elemi téglalap mezőinek kiválasztásától függ, míg az elemi téglalapok bármely más mezőjére írt számot már az elemi téglalapon kívül elhelyezkedő mezők kiválasztása is befolyásolja.) Tehát minden elemi téglalap kiszámolható. Mivel $n = 3 k + 1$ szép, azért a teljes sakktábla felbontható elemi téglalapokra a 2. ábrán látható módon. Tehát a teljes sakktábla kiszámolható. Ebből következik, hogy a sakktábla egy része pontosan akkor kiszámolható, ha a komplementere kiszámolható. Könnyen látható, hogy tetszőleges szép sor, illetve szép oszlop komplementere felbontható elemi téglalapokra, így a szép sorok és oszlopok kiszámolhatók. Tekintsünk egy szép mezőt. Ha az ezt tartalmazó sort és oszlopot is elhagyjuk, a megmaradt rész felbontható elemi téglalapokra (3. ábra). Ezért az adott mezőt tartalmazó sor és oszlop egyesítéséből álló ,,kereszt'' kiszámolható. Ha a sorban lévő kiválasztott mezők számához hozzáadjuk az oszlopban lévő kiválasztott mezők számát, majd kivonjuk a keresztben lévő kiválasztott mezők számát, az eredmény pontosan akkor lesz 1, ha a ,,kereszt'' közepe szerepel a kiválasztottak között. Ezért minden egyes szép mező kiszámolható.

1. ábra

2. ábra

3. ábra

Most megmutatjuk, hogy minden átlagos mező is kiszámolható. A tábla átlóra vonatkozó szimmetriája miatt feltehetjük, hogy a mezőnek a sorindexe szép, vagyis a mező sora kiszámolható. A mező oszlopindexe 3-mal osztva 0 vagy 2 maradékot ad, ennek megfelelően vagy a tőle közvetlenül jobbra, vagy a tőle közvetlenül balra lévő oszlop szép. Tekintsük azt a dupla oszlopot, amely ebből a szép oszlopból és a mezőt tartalmazó oszlopból áll (4. ábra). Ennek a dupla oszlopnak a komplementere is felbontható elemi téglalapokra, vagyis a dupla oszlop kiszámolható. Hasonlóképpen, a dupla oszlop és a mezőt tartalmazó sor egyesítésével kapott kereszt is kiszámolható, ezek alapján pedig kiszámolható az az

1 \times 2

-es téglalap is, amely a sor és a dupla oszlop metszeteként áll elő. Ez a téglalap a szóban forgó átlagos mező mellett még egy szép mezőt tartalmaz, amiről már tudjuk, hogy kiszámolható. Ezért a szóban forgó átlagos mező is kiszámolható.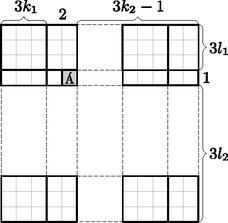

4. ábra

Már csak azt kell igazolni, hogy a csúnya mezők is kiszámolhatók. Bármely ilyen mező sarkosan érintkezik egy szép mezővel, és ezek együtt egy olyan

2 \times 2

-es négyzet két átellenes sarokmezőjét alkotják, melyben a másik két mező átlagos (5. ábra). Elég tehát azt megmutatnunk, hogy ez a

2 \times 2

-es négyzet kiszámolható. Ez rögtön következik abból, hogy az őt tartalmazó dupla sor, dupla oszlop, és az e kettő egyesítéseként kapott kereszt is kiszámolható, mert mindegyikük komplementere elemi téglalapokra bontható.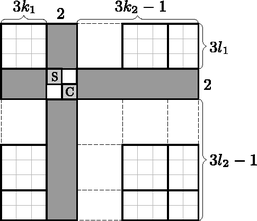

5. ábra

Ezzel beláttuk, hogy a táblázat valamennyi mezője kiszámolható és így azt is meg tudjuk mondani, hogy melyek a kiválasztott mezők.