Kezdőlap


Feladat:	B.4143	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	2009/október, 408 - 410. oldal		PDF \| MathML
Témakör(ök):	Mértani helyek, Kör geometriája, Szélsőérték-feladatok, Trigonometrikus függvények, Feladat
Hivatkozás(ok):	Feladatok: 2009/január: B.4143

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A négyzet másik két csúcsa a kör középponttól ugyanolyan távolságra van a szimmetria miatt. Az egyszerű megoldás kulcsa a feladat következő átfogalmazása:
Adott egy egység sugarú $k$ kör és annak egy $A$ pontja. A pozitív körüljárású $A B C D$ négyzet $B$ csúcsa a $k$ körre illeszkedik. Mi a $D$ csúcsnak a kör $O$ középpontjától való lehetséges legkisebb és legnagyobb távolsága?
A $D$ csúcsot a $B$ -ből $A$ körüli pozitív irányú $90^{\circ}$ -os forgatással kapjuk. Ezért amikor a $B$ csúcs befutja a $k$ kör $A$ -tól különböző pontjait, a $D$ csúcs mértani helye azon $O'$ középpontú $k'$ kör $A$ -tól különböző pontjaiból áll, amelyet a $k$ -ból ugyancsak $A$ körüli pozitív irányú $90^{\circ}$ -os forgatás hoz létre (1. ábra). Az extremális helyzetben lévő $D$ pontok az $O O'$ egyenesen helyezkednek el. Mivel az $O A O'$ háromszög egyenlőszárú és derékszögű, azért $O O' = \sqrt[]{2}$ . Tehát a $D$ pontnak $O$ -tól való lehetséges legkisebb távolsága $\sqrt[]{2} - 1$ , lehetséges legnagyobb távolsága pedig $\sqrt[]{2} + 1$ .

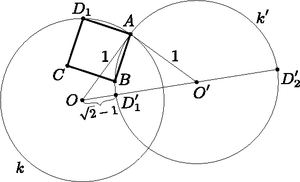1. ábra

II. megoldás. Vegyünk fel egy derékszögű koordinátarendszert úgy, hogy az origó az adott kör

O

középpontja legyen, a négyzet körre illeszkedő két csúcsának koordinátái pedig

A (cos t, sin t)

és

B (cos t, - sin t)

legyenek, ahol

0 < t \leq π / 2

(2. ábra).

2. ábra

Ekkor a négyzet oldalai párhuzamosak a koordinátatengelyekkel, hosszuk pedig

2 sin t

. Ezért a másik két csúcs koordinátái vagy

C_{j} (cos t + 2 sin t, - sin t)

és

D_{j} (cos t + 2 sin t, sin t)

, vagy pedig

C_{b} (cos t - 2 sin t, - sin t)

és

D_{b} (cos t - 2 sin t, sin t)

, attól függően, hogy a csúcsok az

A B

egyenesnek

O

-val megegyező, vagy azzal ellentétes oldalán vannak. Nyilván igaz, hogy

O C_{j} = O D_{j} \geq O C_{b} = O D_{b}

, ezért a távolság maximumát az

O C_{j}

, minimumát pedig az

O D_{b}

típusú szakaszok közt kell keresnünk. Mivel a pozitív számok körében a négyzetreemelés megtartja a nagyság szerinti rendezést, elég a távolságok négyzetének szélsőértékeit meghatároznunk. Vagyis egyrészt az

\begin{matrix} O C_{j}^{2} = {(0 - (cos t + 2 sin t))}^{2} + {(0 + sin t)}^{2} = c (t) \end{matrix}

függvény legnagyobb, másrészt az

\begin{matrix} O D_{b}^{2} = {(0 - (cos t - 2 sin t))}^{2} + {(0 - sin t)}^{2} = d (t) \end{matrix}

függvény legkisebb értékét kell meghatároznunk, mindkétszer a

0 < t \leq π / 2

intervallumon.
Ismert trigonometriai azonosságokat felhasználva kapjuk, hogy

\begin{matrix} c (t) & = {(cos t + 2 sin t)}^{2} + sin^{2} t = 1 + 4 sin^{2} t + 4 sin t cos t = \\ = 1 + 4 \sqrt[]{2} sin t (\frac{\sqrt[]{2}}{2} sin t + \frac{\sqrt[]{2}}{2} cos t) = 1 + 4 \sqrt[]{2} sin t sin (t + π / 4) = \\ = 1 + 2 \sqrt[]{2} (cos (t - (t + π / 4)) - cos (t + (t + π / 4))) = \\ = 1 + 2 \sqrt[]{2} (\frac{\sqrt[]{2}}{2} - cos (2 t + π / 4)) = 3 - 2 \sqrt[]{2} cos (2 t + π / 4), \end{matrix}

illetve

\begin{matrix} d (t) & = {(cos t - 2 sin t)}^{2} + sin^{2} t = 1 + 4 sin^{2} t - 4 sin t cos t = \\ = 1 + 4 \sqrt[]{2} sin t (\frac{\sqrt[]{2}}{2} sin t - \frac{\sqrt[]{2}}{2} cos t) = 1 + 4 \sqrt[]{2} sin t sin (t - π / 4) = \\ = 1 - 2 \sqrt[]{2} (cos (t + (t - π / 4)) - cos (t - (t - π / 4))) = \\ = 1 - 2 \sqrt[]{2} (cos (2 t - π / 4) - \frac{\sqrt[]{2}}{2}) = 3 - 2 \sqrt[]{2} cos (2 t - π / 4) . \end{matrix}

Mivel minden

x

értékre igaz, hogy

- 1 \leq cos x \leq 1

, azért

\begin{matrix} c (t) \leq 3 + 2 \sqrt[]{2} és d (t) \geq 3 - 2 \sqrt[]{2} . \end{matrix}

0 < t \leq π / 2

, akkor mindkét egyenlőtlenségben pontosan egyszer áll fenn egyenlőség,

t = 3 π / 8

, illetve

t = π / 8

esetén. Tehát

c (t)

maximuma

3 + 2 \sqrt[]{2} = {(1 + \sqrt[]{2})}^{2}

d (t)

minimuma pedig

3 - 2 \sqrt[]{2} = = {(\sqrt[]{2} - 1)}^{2}

.
Vagyis a négyzet másik két csúcsának

O

-tól való távolsága legalább

\sqrt[]{2} - 1

és legfeljebb

\sqrt[]{2} + 1

Megjegyzés. Az I., ,,egyszerű'' megoldásra persze nehéz rájönni. A feladat ,,szokásos'' megoldása a II. megoldás. Ebben a megoldásban a

c (t)

és

d (t)

függvények szélsőértékeit deriválással is meg lehet határozni.