| Feladat: | B.4159 | Korcsoport: 16-17 | Nehézségi fok: átlagos |
| Megoldó(k): | Csere Kálmán | ||
| Füzet: | 2009/szeptember, 340. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Feladat, Középpontos tükrözés, Háromszög nevezetes körei, Síkgeometriai szerkesztések | ||
| Hivatkozás(ok): | Feladatok: 2009/február: B.4159 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Megoldás. Tudjuk, hogy azon pontok mértani helye, melyekre adott esetén teljesül, az adott arányhoz tartozó Apollóniusz-kör. (Ennek bizonyítása, valamint az Apollóniusz-kör szerkesztésének leírása megtalálható pl. a Geometriai feladatok gyűjteménye I. kötetének 1395. és 1396. feladataiban.) Esetünkben . Az Apollóniusz-kör egyenesen lévő átmérőjének végpontjai ezért a pontnak -ra vonatkozó tükörképe, illetve az szakasz -hoz közelebbi harmadolópontja. 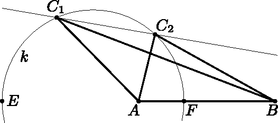 Ezek alapján a keresett pont szerkesztése: Megszerkesztjük -nek -ra vonatkozó tükörképét és az szakasz -hoz közelebbi harmadolópontját, majd pedig az szakasz Thalész-körét. Ennek a körnek és az adott egyenesnek a metszéspontja a háromszög harmadik csúcsa. Az így szerkesztett háromszögben nyilván teljesül. A feladatnak nincs megoldása, ha és egybeesik. Ha , akkor a megoldások száma 0, 1 vagy 2, attól függően, hogy -nek és -nak hány olyan közös pontja van, ami különbözik -től is és -től is. |