Kezdőlap


Feladat:	B.4135	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bodor Bertalan , Nagy Róbert
Füzet:	2009/szeptember, 337. oldal		PDF \| MathML
Témakör(ök):	Négyzetek, Síkgeometriai számítások trigonometriával, Feladat
Hivatkozás(ok):	Feladatok: 2008/december: B.4135

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen a négyzet oldala egységnyi hosszú.

Nyilván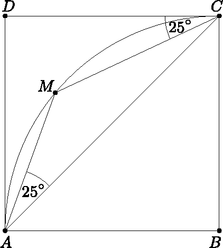

\begin{matrix} A C M ∢ & = A C D ∢ - M C D ∢ = 45^{\circ} - 25^{\circ} = 20^{\circ}, \\ B A M ∢ & = B A C ∢ + C A M ∢ = 45^{\circ} + 25^{\circ} = 70^{\circ}, \\ A M C ∢ & = 180^{\circ} - A C M ∢ - C A M ∢ = 135^{\circ} . \end{matrix}

A C M

háromszögre felírt szinusz-tételből:

\begin{matrix} A M = \frac{sin 20^{\circ}}{sin 135^{\circ}} \cdot A C = \frac{sin 20^{\circ}}{\frac{1}{\sqrt[]{2}}} \cdot \sqrt[]{2} = 2 sin 20^{\circ} . \end{matrix}

A B M

háromszögben a

B M

oldalra a koszinusz-tételt felírva:

\begin{matrix} B M^{2} = A M^{2} + A B^{2} - 2 A B \cdot A M \cdot cos 70^{\circ} = 4 sin^{2} 20^{\circ} + 1 - 4 sin 20^{\circ} cos 70^{\circ} = 1. \end{matrix}

Tehát

B M = 1

, és így az

A B M

háromszög egyenlő szárú:

A B = B M

, vagyis

B M A ∢ = B A M ∢ = 70^{\circ}

. Ebből pedig

A B M ∢ = 40^{\circ}

következik.

II. megoldás. Az ábrát megrajzolva sejthető, hogy az

A M C

háromszög körülírt körének

B

a középpontja.

Először ezt látjuk be. Jelölje az

A M C

háromszög körülírt körét

k

, középpontját

O

. A

k

körben az

M C

ívhez tartozó kerületi szög

M A C ∢ = 25^{\circ}

. Mivel

M C D ∢ = 25^{\circ}

, ez a szög az

M C

ív érintő szárú kerületi szöge, és így

C D

k

kör

C

-beli érintője. Emiatt

C D ⊥ C O

, vagyis

O

illeszkedik a

B C

egyenesre.
Ugyanakkor

O

rajta van a

C A

szakasz felező merőlegesén is, ami a

B D

egyenes.
Tehát

O

B C

és a

B D

egyenes metszéspontja, vagyis a

B

pont.
Ebből következik, hogy

B A = B M

, azaz a

B A M

háromszög egyenlő szárú. Tudjuk, hogy

B A M ∢ = 25^{\circ} + 45^{\circ} = 70^{\circ}

, tehát

A B M ∢ = 180^{\circ} - 2 \cdot 70^{\circ} = 40^{\circ}