Kezdőlap


Feladat:	C.833	Korcsoport: 14-15	Nehézségi fok: átlagos
Füzet:	2007/április, 214 - 215. oldal		PDF \| MathML
Témakör(ök):	Térgeometriai számítások trigonometria nélkül, Szabályos sokszög alapú gúlák, Pitagorasz-tétel alkalmazásai, C gyakorlat
Hivatkozás(ok):	Feladatok: 2005/december: C.833

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Az alaplap oldaléleinek hossza, ami egyben a gúla magassága, $a = m = 40$ cm. Az alaplap átlója $d = a \sqrt[]{2}$ , a gúla oldalélét jelölje $x$ . A gúla magasságának egyenese az alaplapot az átlók felezőpontjában, $O$ -ban döfi. A gúla csúcsai legyenek $A$ , $B$ , $C$ , $D$ , $E$ az 1. ábra szerint. Az $E O C$ háromszögben írjuk fel Pitagorasz tételét: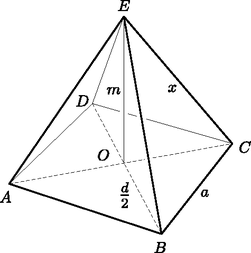

\begin{matrix} x^{2} = {(\frac{a \sqrt[]{2}}{2})}^{2} + m^{2}, \end{matrix}

m = a

miatt

x = a \sqrt[]{\frac{3}{2}}

1. ábra

A B E

és

B C E

háromszöglapokat az

E B

él körül hajtsuk ki egy síkba (2. ábra) . Az

A B = B C = a

A E = B E = C E = x

E A B ∢ = A B E ∢ = E B C ∢ = E C B ∢

egyenlőségekből következik, hogy az

A' B C' E

idom deltoid. Az

A'

és

C'

pont közötti legrövidebb út az őket összekötő szakasz, vagyis a deltoid

A' C'

átlója. Ennek hosszát kell kiszámítani.

2. ábra

A' B E

háromszögben az

A' B

oldalhoz tartozó magasság

m_{1}

; mivel

A' T = T B = \frac{a}{2}

, a Pitagorasz-tételből:

\begin{matrix} m_{1} = \sqrt[]{x^{2} - {(\frac{a}{2})}^{2}} = \sqrt[]{a^{2} \frac{3}{2} - \frac{a^{2}}{4}} = a \sqrt[]{\frac{5}{4}} . \end{matrix}

Tudjuk, hogy a deltoid területe fele az átlói szorzatának. Írjuk fel a deltoid

T

területét, ami nem más, mint az

A' B E

háromszög területének kétszerese, hiszen

A' B E ▵ ≅ B C' E ▵

.
Az

A' B E

háromszög területe

\frac{a m_{1}}{2}

, ezért

T = a m_{1}

, másrészt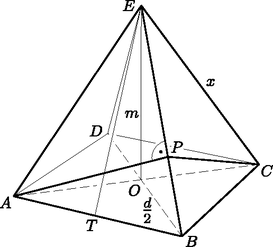

T = \frac{x \cdot A' C'}{2}

, azaz

\begin{matrix} a m_{1} = \frac{x \cdot A' C'}{2} . \end{matrix}

Innen

\begin{matrix} A' C' = \frac{2 a m_{1}}{x} . \end{matrix}

Helyettesítsük be

m_{1}

és

x

előbb kiszámított értékeit, így kapjuk, hogy

\begin{matrix} A' C' = 2 a \frac{a \sqrt[]{\frac{5}{4}}}{a \sqrt[]{\frac{3}{2}}} = 2 a \sqrt[]{\frac{5}{6}} \approx 73, 03 cm. \end{matrix}

II. megoldás. Tudjuk, hogy egy pont és egy egyenes távolsága a pontból az egyenesre állított merőleges szakasz hossza. Állítsunk

A

-ból és

C

-ből merőlegest a két háromszög közös

E B

élére (3. ábra). Az

A E B

és

C E B

háromszögek egybevágóságából következik, hogy a két merőleges ugyanabban a

P

pontban metszi az

E B

élt. Az

A P

távolságot meghatározhatjuk az

E T B

és

A P B

háromszögek hasonlóságából, mindkettő derékszögű, és

E B A

szögük közös (4. ábra). Vagyis

\begin{matrix} \frac{A P}{m_{1}} = \frac{a}{x}, \end{matrix}

innen

A P = \frac{a m_{1}}{x}

ennek kétszerese pedig megegyezik az előbb kapott

A' C'

értékével. (Hiszen

A P + P C

nem más, mint az előzőkben síkba fektetett deltoid átlója.) Innen ugyanúgy folytathatjuk a számítást, mint az I. megoldásnál.

3. ábra

4. ábra