Kezdőlap


Feladat:	B.3846	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Herber Máté , Horváth Gábor , Nagy Réka
Füzet:	2007/február, 91 - 93. oldal		PDF \| MathML
Témakör(ök):	Irracionális egyenletek, Feladat
Hivatkozás(ok):	Feladatok: 2005/október: B.3846

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Mindkét oldalt négyzetre emelve, majd rendezve:

\begin{matrix} \sqrt[]{2 - x} + \sqrt[]{15 + x} = 9 - 2 \sqrt[4]{(2 - x) (15 + x)} . \end{matrix}

Ismét négyzetre emelve:

\begin{matrix} (2 - x) + (15 + x) + 2 \sqrt[]{(2 - x) (15 + x)} = \\ = 81 + 4 \sqrt[]{(2 - x) (15 + x)} - 36 \sqrt[4]{(2 - x) (15 + x)} . \end{matrix}

Legyen

a = \sqrt[4]{(2 - x) (15 + x)}

. Ekkor

\begin{matrix} 17 + 2 a^{2} & = 81 + 4 a^{2} - 36 a, \\ 0 & = 2 a^{2} - 36 a + 64. \end{matrix}

Innen

a = 16

vagy

a = 2

.
Ha

a = 16

, akkor a

16 = \sqrt[4]{(2 - x) (15 + x)}

egyenlet mindkét oldalát negyedik hatványra emelve, majd rendezve a

0 = x^{2} + 13 x + 65 506

egyenletet kapjuk. Ennek negatív a diszkriminánsa, tehát nincs megoldása.
Ha

a = 2

, akkor a

2 = \sqrt[4]{(2 - x) (15 + x)}

egyenlet mindkét oldalát negyedik hatványra emelve, majd rendezve a

0 = x^{2} + 13 x - 14

egyenletet kapjuk. Ennek megoldása

x_{1} = - 14

és

x_{2} = 1

, mindkét gyök megoldása az eredeti egyenletnek is.

II. megoldás. Legyen

a = \sqrt[4]{2 - x}

b = \sqrt[4]{15 + x}

. Ekkor

a + b = 3

, valamint

a^{4} + b^{4} = 17

. Írjuk fel az

{(a + b)}^{4}

hatványt, majd alakítsuk át:

\begin{matrix} {(a + b)}^{4} = a^{4} + 4 a^{3} b + 6 a^{2} b^{2} + 4 a b^{3} + b^{4} = 17 + 4 a^{3} b + 6 a^{2} b^{2} + 4 a b^{3} . \end{matrix}

Felhasználva, hogy

{(a + b)}^{4} = 81

, a következő egyenletet kapjuk:

\begin{matrix} 32 = 2 a^{3} b + 3 a^{2} b^{2} + 2 a b^{3} = a b (2 a^{2} + 3 a b + 2 b^{2}) = a b (2 {(a + b)}^{2} - a b) = a b (18 - a b) . \end{matrix}

A zárójelet felbontva és nullára redukálva:

\begin{matrix} {(a b)}^{2} - 18 a b + 32 = 0. \end{matrix}

Ez az egyenlet

a b

-re nézve másodfokú, megoldása:

a b = 16

, illetve

a b = 2

. Ezekből

a = 3 - b

felhasználásával:

(3 - b) b = 16

, vagy (

3 - b) b = 2

. Így

b

-re két másodfokú egyenletet kapunk. Az elsőnek a diszkriminánsa negatív, tehát nincs valós gyöke. A második egyenletből:

b_{1} = 2

b_{2} = 1

. Innen:

\sqrt[4]{15 + x} = 2

x_{1} = 1

;

\sqrt[4]{15 + x} = 1

x_{2} = - 14

. Mindkét

x

érték megoldása az eredeti egyenletnek is.

III. megoldás. Legyen

\begin{matrix} f (x) = \sqrt[4]{2 - x} + \sqrt[4]{15 + x}, \end{matrix}

ahol

x \in [- 15,2]

. Végezzünk függvényvizsgálatot. Számítsuk ki először az elsőrendű deriváltat:

\begin{matrix} f' (x) & = \frac{1}{4} \cdot \frac{1}{\sqrt[4]{{(2 - x)}^{3}}} \cdot (- 1) + \frac{1}{4} \cdot \frac{1}{\sqrt[4]{{(15 + x)}^{3}}} \cdot (+ 1) = \\ = \frac{1}{4} \cdot (\frac{1}{\sqrt[4]{{(15 + x)}^{3}}} - \frac{1}{\sqrt[4]{{(2 - x)}^{3}}}) . \end{matrix}

Ez csak akkor lehet 0, ha

x \neq - 15

és

x \neq 2

mellett

\begin{matrix} \frac{1}{\sqrt[4]{{(15 + x)}^{3}}} = \frac{1}{\sqrt[4]{{(2 - x)}^{3}}}, \\ 15 + x = 2 - x, x = - 6, 5. \end{matrix}

Felhasználva, hogy a

] - 15; 2 [

intervallumon az

f' (x)

végig értelmezve van, és pl.

f' (- 7) > 0

, és

f' (0) < 0

, kapjuk, hogy

f' (x)

] - 15; - 6, 5 [

intervallumon pozitív, így itt

f (x)

szigorúan monoton nő; a

] - 6, 5; 2 [

intervallumon negatív, így itt

f (x)

szigorúan monoton csökken; végül mivel

f' (x)

- 6, 5

-ben 0, és előjelet vált, így itt

f (x)

-nek maximuma van. Ennek értéke:

f (- 6, 5) \approx 3, 415 > 3

. Tehát az

f

függvény két helyen veszi föl a 3-at az adott intervallumon. Mivel

f (1) = f (- 14) = 3

, és

f (- 15) = f (2) \approx 2, 03

, azért az egyenletnek két megoldása van: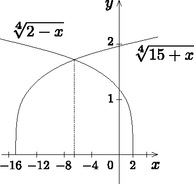

x = 1

és

x = - 14

Megjegyzés. Ábrázolva

f (x)

két tagját külön-külön, az ábráról sejthető, hogy a metszéspontban (

x = - 6, 5

) lesz a két függvény összegének értéke maximális, hiszen a metszéspontra szimmetrikus a két függvény, és pl. a metszésponttól jobbra

\sqrt[4]{2 - x}

,,jobban'' csökken, mint amennyire

\sqrt[4]{15 + x}

nő.

Valóban, mivel a

g (x) = \sqrt[4]{x}

függvény szigorúan konkáv, azért az

f

függvény értéke

- 6, 5

-nél kisebb, illetve nagyobb

x

-ekre:

\begin{matrix} f (- 6, 5 + ε) = f (- 6, 5 - ε) = \sqrt[4]{8, 5 - ε} + \sqrt[4]{8, 5 + ε} = \\ = 2 \cdot [0, 5 \cdot \sqrt[4]{8, 5 - ε} + 0, 5 \cdot \sqrt[4]{8, 5 + ε}], \end{matrix}

ami a Jensen-egyenlőtlenség szerint

ε > 0

miatt kisebb, mint

\begin{matrix} 2 \cdot \sqrt[4]{0, 5 \cdot 2 \cdot 8, 5} = 2 \cdot \sqrt[4]{8, 5} = f (- 6, 5) . \end{matrix}

Ezzel csak azt mutattuk meg, hogy az

f (x)

függvény

x = - 6, 5

-nél veszi fel a maximumát, azt nem, hogy minden más értéket a

[- 15; 6, 5 [

és a

[- 6, 5; 2]

intervallumban is csak egyszer-egyszer vesz föl. Ha megnézzük a

g (x) = \sqrt[4]{x}

grafikonját, látható, hogy ,,jobbra'' haladva a növekedése lelassul, amiből már következik, hogy

δ > ε

esetén

\begin{matrix} f (- 6, 5 + δ) < f (- 6, 5 + ε) . \end{matrix}

(

\sqrt[4]{8, 5 - δ} + \sqrt[4]{8, 5 + δ} < \sqrt[4]{8, 5 - ε} + \sqrt[4]{8, 5 + ε}

\sqrt[4]{8, 5 + δ} - \sqrt[4]{8, 5 + ε} < \sqrt[4]{8, 5 - ε} - \sqrt[4]{8, 5 - δ}

, ami az ábrán szemléltetett két szakaszhoz hasonlóan ábrázolható.)

Pontos bizonyítás a III. megoldásban is használt deriválással adható.