Kezdőlap


Feladat:	4111. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Boros Csanád Örs , Budai Ádám , Deák Zsolt , Emroz Khan , Farkas Márton , Filep Tibor , Hartstein Máté , Iván Dávid , Marák Károly , Szabó Dávid , Wang Daqian
Füzet:	2009/április, 244 - 247. oldal		PDF \| MathML
Témakör(ök):	Feladat, Hajítások
Hivatkozás(ok):	Feladatok: 2008/november: 4111. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A traktorkeréken lévő sárdarab ‐ még a leválása előtt ‐ $v$ sebességű vízszintes irányú haladó mozgást és $\frac{2 v}{D}$ szögsebességű forgómozgást végez. Amikor a sárdarab leválik a kerékről, akkor (a leválás helye által meghatározott $h$ magasságból és meghatározott kezdősebességgel indulva) ferde hajításnak megfelelően mozog tovább. A levegőben töltött $t$ időt a $h$ magasság és a kezdősebesség függőleges komponense határozza meg, a vízszintes mozgás az esési idő szempontjából érdektelen.

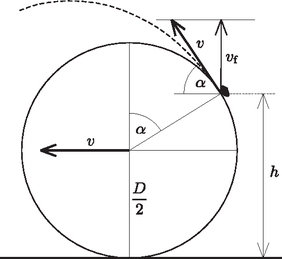1. ábra

Vizsgáljuk azt az esetet, amikor a sárdarab az 1. ábrán látható, az

α

szöggel jellemezhető helyzetben válik el a keréktől. A sárdarab magassága ekkor

\begin{matrix} h = \frac{D}{2} (1 + cos α), \end{matrix}

kezdősebességének függőleges komponense pedig

\begin{matrix} v_{f} = v sin α . \end{matrix}

A levegőben töltött időt ‐ bármilyen

α

szög esetén ‐ a függőleges mozgásra felírható

\begin{matrix} - \frac{g}{2} \cdot t^{2} + v_{f} \cdot t = - h, \end{matrix}

(1)

vagyis a

\begin{matrix} - \frac{g}{2} \cdot t^{2} + v sin α \cdot t = - \frac{D}{2} (1 + cos α) \end{matrix}

(2)

egyenletből (annak pozitív gyökét választva) határozhatjuk meg:

\begin{matrix} t (α) = \frac{v}{g} [sin α + \sqrt[]{sin^{2} α + \frac{D g}{v^{2}} (1 + cos α)}] . \end{matrix}

(3)

t (α)

függvény maximumát (vagyis a leghosszabb esési időt) differenciálszámítással, (3) jobb oldalának

α

szerinti deriválásával határozhatjuk meg. A szélsőértéknél a derivált eltűnik:

\begin{matrix} \frac{d t (α)}{d α} = \frac{v}{g} [cos α + \frac{sin α cos α - \frac{D g}{2 v^{2}} sin α}{\sqrt[]{sin^{2} α + \frac{D g}{v^{2}} (1 + cos α)}}] = 0. \end{matrix}

A fenti egyenletből algebrai átalakításokkal kapjuk:

\begin{matrix} \frac{D g}{2 v^{2}} sin α - sin α cos α = cos α \sqrt[]{sin^{2} α + \frac{D g}{v^{2}} (1 + cos α)}, \\ {(\frac{D g}{2 v^{2}} sin α - sin α cos α)}^{2} = cos^{2} α \cdot [sin^{2} α + \frac{D g}{v^{2}} (1 + cos α)], \\ {(\frac{D g}{2 v^{2}})}^{2} sin^{2} α - \frac{D g}{v^{2}} sin^{2} α \cdot cos α = \frac{D g}{v^{2}} (1 + cos α) cos^{2} α, \\ (\frac{D g}{4 v^{2}} - cos α) \cdot sin^{2} α = (1 + cos α) \cdot cos^{2} α . \end{matrix}

Innen a

\begin{matrix} sin^{2} α = (1 + cos α) \cdot (1 - cos α) \end{matrix}

azonosság és

1 + cos α \neq 0

felhasználásával kapjuk, hogy

\begin{matrix} (\frac{D g}{4 v^{2}} - cos α) \cdot (1 - cos α) = cos^{2} α, \end{matrix}

vagyis

\begin{matrix} \frac{D g}{4 v^{2}} - \frac{D g}{4 v^{2}} \cdot cos α - cos α = 0, \end{matrix}

azaz

\begin{matrix} cos α = \frac{g D}{g D + 4 v^{2}} . \end{matrix}

(4)

Ez az összefüggés határozza meg a leghosszabb repülési időhöz tartozó

α

,,sárleválási helyzetet''. (4)-et (3)-ba visszahelyettesítve további algebrai átalakítások után a repülési idő maximumális értékére a

\begin{matrix} t_{max} = \frac{\sqrt[]{4 v^{2} + 2 g D}}{g} \end{matrix}

formulát kapjuk.

II. megoldás. A feladatot elemi úton (differenciálszámítás nélkül) is meg lehet oldani. Induljunk ki (az I. megoldás jelöléseit használva) a függőleges hajítás (2) egyenletéből, melyet átrendezéssel

\begin{matrix} \frac{g}{2} \cdot t^{2} - \frac{D}{2} = + v sin α \cdot t + \frac{D}{2} cos α \end{matrix}

(5)

alakra hozhatunk. Nyilván elegendő a

0 < α < 180^{\circ}

esetekkel foglalkoznunk, ezekre pedig ‐ tetszőleges

a

és

b

pozitív számokkal ‐ érvényes az

\begin{matrix} a sin α + b cos α \leq \sqrt[]{a^{2} + b^{2}} \end{matrix}

egyenlőtlenség.

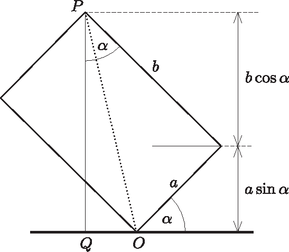2. ábra

Tekintsük ugyanis a 2. ábrán látható,

a

és

b

oldalélű téglalapot, amelynek egyik (

O

jelű) csúcsa egy egyenesre illeszkedik. A téglalap ,,átellenes''

P

csúcsának és az egyenesnek

P Q

távolsága nem lehet nagyobb, mint a

P O

átló

\sqrt[]{a^{2} + b^{2}}

hossza; és ez éppen a belátandó egyenlőtlenség. Az ábráról azt is leolvashatjuk, hogy egyenlőség

\begin{matrix} tg α = \frac{a}{b} \end{matrix}

esetben áll fenn, ekkor a

P O

átló merőleges a szóbanforgó egyenesre.
Alkalmazzuk az egyenlőtlenséget az (5) egyenlet jobb oldalára

a = v t

és

b = \frac{D}{2}

megfeleltetéssel:

\begin{matrix} \frac{g}{2} \cdot t^{2} - \frac{D}{2} \leq \sqrt[]{{(v t)}^{2} + {(\frac{D}{2})}^{2}}, \end{matrix}

(6)

megjegyezve, hogy az egyenlőség

\begin{matrix} tg α = \frac{2 v t}{D} \end{matrix}

(7)

esetén teljesül. (6) négyzetre emelése és átrendezés után a repülési időre a

\begin{matrix} t \leq \frac{\sqrt[]{4 v^{2} + 2 g D}}{g} \end{matrix}

korlátot kapjuk, melynek határeseti értékét (7)-be helyettesítve a keresett szöget is kiszámíthatjuk:

\begin{matrix} tg α = \sqrt[]{{(\frac{4 v^{2}}{g D})}^{2} + \frac{8 v^{2}}{g D}} . \end{matrix}

Ez egyenértékű az I. megoldás (4) formulájával.

(G. P.)

Megjegyzés. A megoldás teljességéhez az is hozzá tartozik, hogy megvizsgáljuk, vajon a kerékről levált sárdarab nem esik-e vissza a kerékre.

Hartstein Máté megoldása