Kezdőlap


Feladat:	B.4074	Korcsoport: 16-17	Nehézségi fok: nehéz
Füzet:	2009/április, 217 - 218. oldal		PDF \| MathML
Témakör(ök):	Mértani helyek, Thalesz tétel és megfordítása, Feuerbach-kör, Magasságpont, Vektorok skaláris szorzata, Feladat
Hivatkozás(ok):	Feladatok: 2008/március: B.4074

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jelöljük a körvonalat $k$ -val, középpontját $O$ -val, sugarát pedig $r$ -rel. Ha $C$ egybeesik $O$ -val, akkor sohasem keletkezik háromszög, ezért ekkor a mértani hely üres. Ha $C$ a körvonalra esik, akkor Thalész tétele szerint a keletkezett $A B C$ háromszögek $C$ -nél lévő szöge derékszög, azaz a magasságpontjuk mindig $C$ , tehát ekkor a mértani hely egyedül a $C$ pontból áll.

A továbbiakban tegyük fel, hogy a

C

pont

c

távolságra helyezkedik el

O

-tól, ahol

0 < c \neq r

. Legyen

D

O C

félegyenesnek az a pontja, amely

O

-tól

d = r^{2} / c

távolságra van¹. Megmutatjuk, hogy a keresett mértani hely az az

e

egyenes, amely merőleges az

O C

egyenesre és áthalad

D

-n.
Indítsunk

O

-ból helyvektorokat és jelöljük ezeket a megfelelő kisbetűvel, azaz tetszőleges

P

pont esetén legyen

\vec{O P} = p

. Ha az

A B C

háromszög magasságpontja

M

, akkor

M

-et a háromszög csúcsaival összekötő egyenesek merőlegesek a háromszög szemközti oldalaira. Tehát

m -a

merőleges a

c-b

vektorra,

m-b

pedig merőleges a

c-a

vektorra. Mivel

b=-a

, a vektorok skaláris szorzatát használva ezt az

\begin{matrix} (m-a) (c+a) = 0 és (m+a) (c-a) = 0 \end{matrix}

összefüggésekkel fejezhetjük ki. Ezeket összeadva kapjuk, hogy

2 m c -2a^{2}=0

, vagyis

mc= a^{2}

. A

D

definíciójából viszont az következik, hogy

dc= a^{2}

, ezért

mc=dc

, s így

(m-d) c=0

. Az

m-d

vektor tehát merőleges a

c

vektorra, vagyis

M D

merőleges

O C

-re. Ezért az

M

pont rajta van az

e

egyenesen.
Megmutatjuk, hogy az

e

egyenes minden pontja előáll valamely megfelelő háromszög magasságpontjaként. Legyen

E

e

egyenes tetszőleges pontja. A

k

-nak pontosan egy

E C

-re merőleges

A_{E} B_{E}

átmérője létezik. Mivel

E C

nem párhuzamos

e

-vel, az

A_{E}

és

B_{E}

nem eshet az

O C

egyenesre, tehát

A_{E}

B_{E}

, és

C

mindig háromszöget alkot. Ennek a háromszögnek a magasságpontja az előzőekben bizonyítottak szerint illeszkedik

e

-re, s mivel

E C

merőleges

A_{E} B_{E}

-re, azért

E C

-re is. Azaz a magasságpont nem lehet más, mint az

E C

egyenes

e

-vel alkotott

E

metszéspontja.

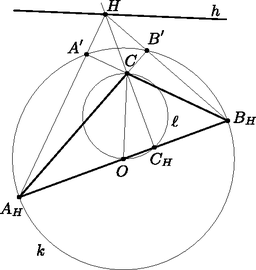
II. megoldás. Használjuk az I. megoldás jelöléseit. Ha

C \equiv O

vagy

C \in k

, akkor ugyanazt mondhatjuk, mint az I. megoldásban. Ha ezek egyike sem teljesül, akkor legyen az

O C

szakasz Thalész-köre

ℓ

, a

k

és

ℓ

hatványvonala²

h

, az

A B C

háromszög magasságainak talppontjai pedig rendre

A'

B'

és

C'

. Megmutatjuk, hogy a keresett mértani hely a

h

egyenes.

A B C

háromszög

f

Feuerbach-köre átmegy az

A'

B'

C'

pontokon, valamint az

M A

M B

M C

szakaszok felezőpontjain. Ezért

M

-nek

f

-re vonatkozó hatványát szelőszakaszok szorzataként felírva kapjuk, hogy

\begin{matrix} A' M \cdot \frac{M A}{2} = B' M \cdot \frac{M B}{2} = C' M \cdot \frac{M C}{2}, \end{matrix}

azaz

\begin{matrix} A' M \cdot M A = B' M \cdot M B = C' M \cdot M C . \end{matrix}

Viszont

A A' B ∢ = B B' A ∢ = O C' C ∢ = 90^{\circ}

, ezért Thalész tételének megfordítása miatt

A'

és

B'

rajta vannak

k

-n,

C'

pedig rajta van

ℓ

-en. Tehát

A' M \cdot M A = B' M \cdot M B

éppen

M

-nek

k

-ra vonatkozó hatványa, míg

C' M \cdot M C

M

-nek

ℓ

-re vonatkozó hatványa. Vagyis

M

-nek a két körre vonatkozó hatványa egyenlő, ezért

M

illeszkedik a körök

h

hatványvonalára.
Be kell még látnunk, hogy

h

minden pontja a mértani helyhez tartozik. Tetszőleges

h

-ra illeszkedő

H

pont esetén legyen

H C

és

ℓ

C

-től különböző metszéspontja

C_{H}

(ez mindig létezik, mert

ℓ

-nek a

C

-beli érintője párhuzamos

h

-val),

k

-nak a

C C_{H}

egyenesre merőleges átmérője pedig

A_{H} B_{H}

. Mivel

C C_{H}

nem párhuzamos

h

-val, azért

A_{H}

B_{H}

, és

C

mindig háromszöget alkot. Ennek a háromszögnek a magasságpontja az előzőekben bizonyítottak szerint illeszkedik

h

-ra, s mivel

C C_{H}

merőleges

A_{H} B_{H}

-ra, így

C C_{H}

-ra is. Azaz a magasságpont nem lehet más, mint a

C C_{H}

egyenes

h

-val alkotott

H

metszéspontja.

¹Ez éppen

C

-nek a

k

-ra vonatkozó inverze.

²A hatványvonalról bővebben lásd: http://www.lexikon.fazekas.hu/.