Feladat: B.4061 Korcsoport: 18- Nehézségi fok: átlagos
Megoldó(k):  Blázsik Zoltán ,  Dinh Hoangthanh Attila ,  Lovas Lia Izabella ,  Tossenberger Anna ,  Varga László 
Füzet: 2009/április, 211 - 214. oldal  PDF  |  MathML 
Témakör(ök): Síkgeometriai bizonyítások, Szögfelező egyenes, Thalesz tétel és megfordítása, Középponti és kerületi szögek, Húrnégyszögek, Feladat
Hivatkozás(ok):Feladatok: 2008/január: B.4061

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jelölje az ABC és a PQR háromszögek szögeit az 1. ábrán látható módon α, β, γ, illetve φ, δ, ε. Mérjük fel az AC oldal A-n túli meghosszabbítására az AB, a PQ oldal P-n túli meghosszabbítására a PR szakaszt. Az így kapott pontok legyenek B', illetve R'. Így a bizonyítandó állítás 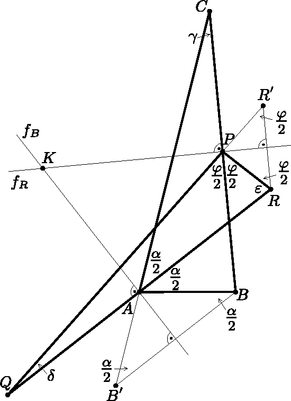B'C=R'Q.
Az AB'B egyenlőszárú háromszög A-nál lévő külső szöge α, ezért

AB'B∢=ABB'∢=α2.
Mivel QR felezi a BAC szöget, BAR∢=α2=ABB'∢, vagyis BB' és RQ párhuzamosak. Ugyanígy kapjuk a PR'R háromszög egyenlőszárúságából kiindulva, hogy RR' és BC is párhuzamosak (1. ábra).
 

 
1. ábra
 

A BB' szakasz felezőmerőlegese, fB átmegy A-n, ami QR felezőpontja, tehát fB egyúttal QR-nek is szakaszfelező merőlegese. Ugyanígy kapjuk, hogy az RR' szakasz felezőmerőlegese, fR átmegy P-n, ami BC felezőpontja, tehát fR egyúttal BC-nek is szakaszfelező merőlegese. Ezért a K=fB∩fR pont a B'BC és az R'RQ háromszögek körülírt köreinek is középpontja.
A B'BC háromszög köré írt körben a BC húrhoz α2 kerületi szög tartozik, ezért a megfelelő középponti szög BKC∢=α. Viszont BAC∢=α, tehát a BC szakasz K-ból és A-ból ugyanakkora szögben látszik, ezért BCKA húrnégyszög. Legyen a köré írható köre k1. Hasonlóan kapjuk, hogy RQKP is húrnégyszög, az e köré írható kör legyen k2 (2. áb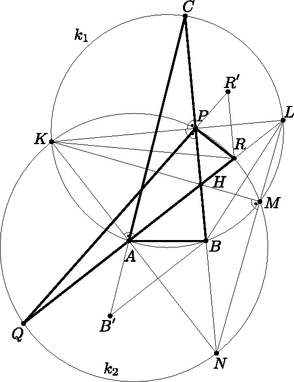ra).
 

 
2. ábra
 

Legyen k1 és k2 második metszéspontja M, KP és k1, illetve KA és k2 második metszéspontja L, illetve N. Mivel KP merőlegesen felezi k1-ben a BC húrt, KL átmérő k1-ben. Ugyanígy kapjuk, hogy KN átmérő k2-ben. Ezért Thalész tétele szerint
LMK∢=NMK∢=90∘,
vagyis L, M és N egy egyenesen vannak. Ugyancsak Thalész tétele miatt KAL∢=90∘, s mivel KA az RQ szakaszfelező merőlegese, A, R és L is egy egyenesen vannak. Ugyanígy látható be, hogy P, B és N is kollineárisak. Ez viszont azt jelenti, hogy a KLN háromszög magasságvonalai éppen KM, LA és NP, azaz e három egyenes a KLN háromszög H magasságpontjában metszi egymást. Ekkor a szelőszakaszok szorzatára vonatkozó tételt (lásd pl. Geometriai feladatok gyűjteménye I, 1325. és 1327. feladatok) H-ra és a k1, illetve k2 körre alkalmazva kapjuk, hogy
BH⋅HC=KH⋅HM,ésRH⋅HQ=KH⋅HM,azazBH⋅HC=RH⋅HQ,
vagyis B, C, R és Q egy k körön vannak. Viszont már láttuk, hogy BC és RQ felezőmerőlegese is átmegy K-n, ezért a négy ponton átmenő kör középpontja K, amiből az következik, hogy k egyúttal a B'BC és R'RQ háromszögek közös körülírható köre.
Most már csak azt kell megmutatnunk, hogy k-ban a B'C és R'Q húrokhoz ugyanakkora kerületi szög tartozik. Ez a szög (lásd az 1. ábrát) k1-ben B'BC∢=α2+β, míg k2-ben R'RQ∢=φ2+ε. Ezek viszont egyenlőek, mert mindkettő megegyezik (180∘-AKP∢)-gel, hiszen AK merőleges B'B-re is és RQ-ra is, PK pedig merőleges BC-re is és R'R-re is. Ezért B'C=R'Q, s így az állítást beláttuk.
 

II. megoldás. Az ABC háromszög köré írható kört jelölje kA, a PQR háromszög köré írhatót pedig kP. A BC egyenesnek a kP körrel alkotott második metszéspontja legyen P', a QR egyenesnek kA-val alkotott második metszéspontja pedig A'. Mivel QPP'∢=RPP'∢, kapjuk, hogy QP'=RP', vagyis AP' a QR szakasz felezőmerőlegese. Hasonlóképpen BA'=CA', és PA' a BC szakasz felezőmerőlegese.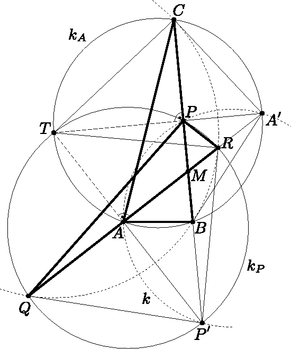
 

 
3. ábra
 

Legyen AP'P∢=ε és P'AB∢=η. Mivel CAA'∢=BAA'∢=90∘-η, azért
CAP'∢=180∘-η,
és így
BA'A∢=BCA∢=η-ε.
Továbbá CA'A∢=CBA∢=ε+η, ahonnan CA'P∢=BA'P∢=η, és PA'A∢=ε következik. Ezért az A', P, A, P' pontok egy k körvonalra illeszkednek, továbbá ha az A'P és P'A egyenesek metszéspontját T-vel jelöljük, akkor
A'TA∢=90∘-ε=BAA'∢+BCA∢=BCA'∢+BCA∢=A'CA∢.
A T pont tehát illeszkedik a kA körre, és ugyanígy a kP körre is, méghozzá TA' a kA körnek, míg TP' a kP körnek átmérője is egyben (3. ábra).
Felhasználva, hogy P'R=P'Q és hogy A felezi a QR szakaszt, valamint Ptolemaiosz tételét (lásd pl. Geometriai feladatok gyűjteménye I, 1259. feladat) a PQP'R húrnégyszögben, kapjuk hogy
(PQ+PR)⋅P'R=PQ⋅P'R+PR⋅QP'=QR⋅PP'=2AR⋅TP'cosε.
Mivel a P'AR és P'RT derékszögű háromszögek P'-nél lévő szöge közös, ezért a háromszögek hasonlók, tehát
PQ+PR=2⋅ARRP'⋅TP'⋅cosε=2⋅RTTP'⋅TP'⋅cosε=2⋅TR⋅cosε,
és ugyanígy kapjuk az A'PC és A'CT háromszögek hasonlóságából, hogy
AB+AC=2⋅TC⋅cosε.
A bizonyítandó állításhoz elegendő tehát a TR=TC egyenlőséget igazolni.
Legyen BC és RQ metszéspontja M. Alkalmazzuk a szelőszakaszok szorzatára vonatkozó tételt az M pontra és rendre a kA, k és kP körökre:
MB⋅MC=MA⋅MA'=MP⋅MP'=MQ⋅MR.
Tehát a B, Q, C és R pontok egy körre esnek. TB=TC és TQ=TR miatt ennek a körnek éppen T a középpontja, vagyis valóban TR=TC. Ezzel az állítást beláttuk.