Feladat: C.937 Korcsoport: 14-15 Nehézségi fok: nehéz
Megoldó(k):  Buzsáki Dániel ,  Dér László ,  Fülöp Dóra ,  Horváth Anna ,  Kis-Pál Tamás 
Füzet: 2009/április, 200 - 204. oldal  PDF  |  MathML 
Témakör(ök): Konvex négyszögek, Oldalak aránya és szögek közötti kapcsolat, Háromszög területe, C gyakorlat
Hivatkozás(ok):Feladatok: 2008/március: C.937

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jelölje az átlók metszéspontját M, az a és a c oldal meghosszabbításának metszéspontját pedig E (1. ábra). Ekkor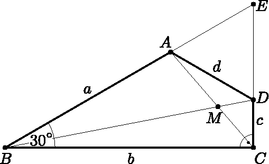

CEB∢=180∘-(EBC∢+BCE∢)=180∘-(30∘+90∘)=60∘.
Vagyis az EBC háromszög egy olyan szabályos háromszög fele, amelynek b a magassága. Így
EB=b32=932=63,ahonnanEA=EB-a=23.
Mivel CE az EB fele, a hossza 33. Ezekből DE=CE-c=23.
 

 
1. ábra
 

Az ADE háromszög két oldala egyenlő, és az általuk bezárt szög 60∘, ezért szabályos. Tehát d=23, EAD∢=ADE∢=60∘, amiből DAB∢=CDA∢=120∘.
Az ABD háromszögben: ABD∢+BDA∢=180∘-DAB∢=60∘. Az ABD és a DAC háromszögek hasonlóak, mert
ABDA=4323=233=DACD
és az ezen két oldal által közbezárt szög DAB∢=CDA∢=120∘. Emiatt ABD∢=DAC∢ is teljesül.
Mindezekből:
AMD∢=180∘-(DAM∢+MDA∢)=180∘-(DAC∢+BDA∢)==180∘-(ABD∢+BDA∢)=180∘-60∘=120∘.

Tehát a négyszög átlói 180∘-120∘=60∘-ot zárnak be egymással.
 
II. megoldás. Az előző megoldásból felhasználjuk, hogy az ABCD négyszög negyedik oldalának hossza 23, és a fennmaradó két szög nagysága pedig 120∘.
Helyezzük el ezt a négyszöget egy ,,szabályos háromszög-rácsban'', ahol a szabályos háromszögek oldalának hossza 23 (2. ábra). Könnyen látható, hogy a magasságuk 3.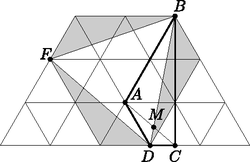
 

 
2. ábra
 

Az ábrán rajzoljuk be az átlókat, majd a rövidebbik átlót toljuk el 3-mal az ábrán látható módon, majd hosszabbítsuk meg, így kapjuk az F pontot. A DBF háromszög szabályos, mert mindhárom oldala egy olyan háromszög leghosszabb oldala, amelynek két rövidebb oldala 23 és 43, és az általuk bezárt szög 120∘-os. Ezért BDF∢=60∘. Az átlók metszéspontját M-mel jelölve BMA∢ és BDF∢ egyállású szögek, ezért BMA∢=60∘, a négyszög átlói által bezárt szög tehát 60∘.
 
III. megoldás. Használjuk az 1. ábra jelöléseit. Legyen továbbá BMA∢=φ. Az I. megoldás szerint BE=63, CE=33 és az ADE háromszög egy 23 oldalú szabályos háromszög, így magassága 3.
Számítsuk ki kétféleképpen a négyszög területét.
T=TBCE-TADE=33⋅92-23⋅32=2132.(1)
Másrészt
T=BD⋅AC2⋅sinφ.(2)
Szükségünk van tehát BD és AC hosszára.
A Pitagorasz-tételből: BD=BC2+CD2=84=221. Az A-ból a BC oldalra állított merőleges talppontját F-fel jelölve látható, hogy a BFA▵ is egy szabályos háromszög fele, amiből BF=6 és
AF=23, továbbá FC=BC-BF=3 következik. Az AFC háromszögre alkalmazott Pitagorasz-tételből kapjuk ezután, hogy
AC=AF2+FC2=21.
Az átlókra kapott értékeket (2)-be helyettesítve:
T=221⋅212⋅sinφ=21sinφ.(3)
Végül (1) és (3) jobb oldalát egyenlővé téve, majd a kapott egyenlet mindkét oldalát 21-gyel osztva kapjuk, hogy sinφ=32, amiből φ=60∘ vagy 120∘, az átlók által bezárt szög tehát 60∘.
 
IV. megoldás. Tekintsük az 1. ábrát.
Legyen BMA∢=α, CBM∢=β és BCM∢=γ. Mivel BMA∢ a BCM háromszög külső szöge, azért α=β+γ. Az ABC háromszögben felírva a koszinusz-tételt:
AC2=48+81-2⋅36⋅3⋅cos30∘=21,
amiből AC=21. A BCD háromszögben felírva a Pitagorasz-tételt: 92+3=BD2, amiből BD=84.
Számoljuk ki β és γ szinuszát és koszinuszát:
sinβ=CDBD=384=127,cosβ=BCBD=984=3327.
Az ABC háromszögre vonatkozó szinusztételből adódóan:
sinγ43=sin30∘21,
amiből sinγ=27. Ebből (mivel γ<90∘) kapjuk, hogy
cosγ=1-47=37.

Végül az addíciós-tételt felhasználva: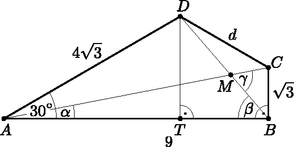
cosα=cos(β+γ)=3327⋅37-127⋅27=12,
és így α=60∘.

 
V. megoldás. Használjuk a 3. ábra jelöléseit.
 

 
3. ábra
 

Mivel γ az ABM háromszög külső szöge, azért γ=α+β. Meghatározásához használjuk fel a
tg(α+β)=tgα+tgβ1-tgα⋅tgβ
összefüggést.
Az ABC háromszögben tgα=39.
Az ATD háromszög egy szabályos háromszög fele, így TD=432=23 és AT=32⋅43=6. Így TB=9-6=3, és a TBD háromszögben tgβ=233.
Így tehát
tgγ=tg(α+β)=39+2331-39⋅233=7392127=3,amibőlα=60∘.

 
VI. megoldás. Állítsunk D-ben merőlegest AD-re, és ennek az AB oldallal vett metszéspontja legyen E. Az ADE háromszögben DAE∢=30∘ és ADE∢=90∘, ezért a háromszög harmadik szöge,
AED∢=60∘, és AD ismeretében DE és AE is meghatározható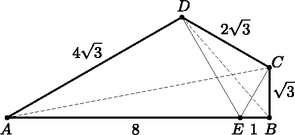: AE=433/2=8, illetve DE=AE/2=4.
 

 
4. ábra
 

Ezután kössük össze az E és a C pontokat. Az EBC háromszög derékszögű, befogói 3 és 1 hosszúak, így átfogója, EC=2, tehát ez a háromszög is egy szabályos háromszög fele, CEB∢=60∘ és
ECB∢=30∘.
A DEC háromszög oldalai: EC=2, ED=4 és CD=23, tehát ez is egy szabályos háromszög fele, DEC∢=60∘, DCE∢=90∘ és EDC∢=30∘.
Tekintsük ezután az ADC és a DCB háromszöget. A két háromszög hasonló, hiszen
ADDC=DCCBésADC∢=DCB∢=90∘+30∘=120∘,
tehát két oldaluk aránya és az általuk közrezárt szög megegyezik. Ez azt jelenti, hogy van olyan középpontos hasonlósági transzformáció, amely az ADC háromszöget a DCB háromszögbe viszi. Mivel az AD és a DC egyenesek által bezárt szög 180∘-120∘=60∘, ezért az AC és a DB egyenesek által bezárt szög is 60∘.