Kezdőlap


Feladat:	B.4052	Korcsoport: 18-	Nehézségi fok: könnyű
Megoldó(k):	Cséke Balázs , Fonyó Dávid
Füzet:	2009/február, 91 - 93. oldal		PDF \| MathML
Témakör(ök):	Gráfelmélet, Konstruktív megoldási módszer, Feladat
Hivatkozás(ok):	Feladatok: 2008/január: B.4052

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Az $n$ csúcsú gráfban jelöljük az ugróiskolához tartozó pontokat $P_{1}, P_{2}, ..., P_{k}$ -val, az egyéb csúcsokat pedig $Q_{k + 1}, ..., Q_{n}$ -nel, ahol minden $i = 1,2, ..., k$ -ra a $P_{i}$ csúcs fokszáma 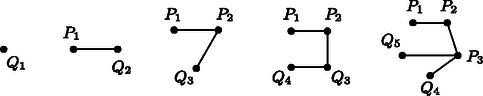$i$ .
A gráf egyszerű, ezért nem lehet benne hurokél és többszörös él. Könnyen belátható, hogy $n = 1,2,3,4,5$ esetben az ugróiskolának rendre 0, 1, 2, 2, 3 csúcsa lehet. Ezeket az eseteket az 1. ábra mutatja be.

1. ábra

A továbbiakban megmutatjuk, hogy

n \geq 6

(

n \in N^{+}

) esetén a feladat feltételeinek megfelelően egy

n

csúcsú gráfban legfeljebb

n - 3

csúcsú ugróiskola alakítható ki.
A

P_{1}, P_{2}, ..., P_{k}

ugróiskola speciálisan egy út, ezért él köti össze a

P_{1} P_{2}

P_{2} P_{3}

...

P_{k - 1} P_{k}

pontpárokat. Először azt látjuk be, hogy a gráfban

k < n - 2

:
Az ugróiskolában

P_{1}

csak

P_{2}

-vel,

P_{2}

pedig csak a

P_{1}

és

P_{3}

csúcsokkal van összekötve. Így,

n - 2 \geq 4

miatt, ha létezne

P_{n - 2}

, akkor sem

P_{1}

-gyel, sem

P_{2}

-vel, sem pedig önmagával nem lehetne összekötve, így fokszáma legfeljebb

n - 3

, azaz

(n - 2)

-nél kevesebb lenne, ami ellentmondás.
Ezután megadunk egy olyan

n

csúcsú gráfot, amelyben létezik

n - 3

csúcspontú ugróiskola. Ehhez az alábbi élek berajzolása szükséges:

$•$	a $P_{1}$ pontot csak $P_{2}$ -vel kötjük össze (fokszáma 1);

$•$	a $P_{2}$ pontot csak $P_{1}$ -gyel és $P_{3}$ -mal kötjük össze (fokszáma 2).

Ezután az ugróiskola utolsó pontjától visszafelé haladva:

$•$	a $P_{n - 3}$ pontot $P_{1}$ , $P_{2}$ és $P_{n - 3}$ kivételével minden ponttal összekötjük (fokszáma $n - 3$ );

$•$	a $P_{n - 4}$ pontot $P_{1}$ , $P_{2}$ , $P_{3}$ és $P_{n - 4}$ kivételével minden ponttal összekötjük (fokszáma $n - 4$ ) stb.;

•

...

;

$•$	páros $n$ esetén: $n = 2 l$ , a $P_{l}$ pontot a $P_{l - 1}$ , $P_{l + 1}$ , $...$ , $P_{2 l - 3} = P_{n - 3}$ , $Q_{2 l - 2}$ , $Q_{2 l - 1}$ pontokkal kötjük össze (fokszáma $l$ );

$•$	páratlan $n$ esetén: $n = 2 l + 1$ , a $P_{l}$ pontot a $P_{l - 1}$ , $P_{l + 1}$ , $...$ , $P_{2 l - 2} = P_{n - 3}$ , $Q_{2 l - 1}$ pontokkal kötjük össze (fokszáma $l$ ).

Így a

P_{3}

pont

P_{2}

P_{4}

P_{n - 3}

-mal lesz összekötve, és fokszáma 3 lesz. A

P_{4}

pont

P_{3}

P_{5}

P_{n - 3}

P_{n - 4}

-gyel lesz összekötve, és fokszáma 4 lesz, és így tovább haladva az index növekedésével egyesével nő a pontok fokszáma is:

$•$	páros $n$ esetén: $n = 2 l$ , a $P_{l - 1}$ pontot a $P_{l - 2}$ , $P_{l + 1}$ , $P_{l + 2}$ , $...$ , $P_{2 l - 3} = P_{n - 3}$ , $Q_{2 l - 2}$ , pontokkal kötjük össze (fokszáma $l - 1$ );

$•$	páratlan $n$ esetén: $n = 2 l + 1$ , a $P_{l - 1}$ pontot a $P_{l - 2}$ , $P_{l + 1}$ , $P_{l + 2}$ , $...$ , $P_{2 l - 2} = P_{n - 3}$ pontokkal kötjük össze (fokszáma $l - 1$ ).

A 2. ábra

n = 12

esetén mutatja be az elkészült gráfot.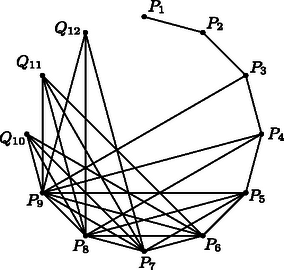

2. ábra

Eredményeinket összefoglalva:

n = 1,2,3,4,5

esetén

k = 0,1,2,2,3

n \geq 6

esetén pedig legfeljebb

n - 3

csúcsú ugróiskola létezhet a feladat feltételeinek megfelelően az

n

csúcspontú egyszerű gráfban.

II. megoldás. Könnyen belátható, hogy

n = 1,2,3,4,5,6,7

esetben az ugróiskolának rendre legfeljebb

k = 0,1,2,2,3,3,4

csúcsa lehet. Sejtésünk, hogy további

n

-ekre

k = n - 3

. Ezt fogjuk bizonyítani.
Először tegyük fel, hogy létezik

n - 2

csúcsú ugróiskola az n csúcsú gráfban. Ekkor a

P_{n - 2}

csúcsból nem mehet él a

P_{1}

-be (hiszen

P_{1}

-ből csak 1 él indulhat ki

P_{2}

-be), nem mehet él a

P_{2}

-be (hiszen

P_{2}

-ből csak két él indul

P_{1}

-be és

P_{3}

-ba) és nem mehet él önmagába (hiszen a gráf egyszerű). Tehát csak

n - 3

él indulhat belőle, ami ellentmondás.
Ezért az ugróiskolának legfeljebb

n - 3

csúcsa lehet. Teljes indukciót alkalmazva megmutatjuk, hogy ez mindig elérhető.
Az állítás

n = 6

-ra és

n = 7

-re igaz.
Tegyük fel, hogy az állítás

(n - 2)

-re igaz, a legnagyobb fokszámú csúcs foka

n - 5

. Ekkor vegyünk fel két új pontot. Az egyik pontot ‐ ez lesz az új gráf

P_{1}

pontja ‐ kössük össze az

n - 2

csúcsú gráf első pontjával; az lesz az új gráf

P_{2}

pontja (fokszáma 2). A másik pontot pedig kössük össze az

n - 2

csúcsú gráf

P_{2}, ..., P_{n - 5}

pontjaival, valamint a megmaradt 3 csúccsal (

n - 4

n - 3

és

n - 2

). Ekkor ezen pont fokszáma:

(n - 5) - 1 + 3 = n - 3

lesz, tehát ez lesz az új gráfban a

P_{n - 3}

pont. A régi gráf

P_{2}, ..., P_{n - 5}

pontjainak fokszáma eggyel nő, ezek lesznek az új gráf

P_{3}, ..., P_{n - 4}

pontjai.
Az így létrehozott új gráf

P_{1}, ..., P_{n - 3}

pontjai a feltételeknek megfelelő ugróiskolát alkotnak az

n

csúcsú gráfban.
Beláttuk, hogy az állítás

(n - 2)

-ről

n

-re öröklődik, így a teljes indukció elvéből következően

n = 6

, illetve

n = 7

esetekből kiindulva minden

n

-re igaz.