Kezdőlap


Feladat:	B.4080	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Ágoston Tamás , Balla Attila , Reiter Viktor , Strenner Péter
Füzet:	2009/január, 27. oldal		PDF \| MathML
Témakör(ök):	Geometriai valószínűség, Háromszög területe, Indirekt bizonyítási mód, Feladat
Hivatkozás(ok):	Feladatok: 2008/március: B.4080

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Tegyük fel az egyszerűség kedvéért, hogy a kör kerülete egységnyi, és legyen $A$ a körvonal egy rögzített pontja. Szimmetria okok miatt a keresett valószínűség megegyezik annak a valószínűségével, hogy ha egymástól függetlenül egy $B$ és egy $C$ pontot kiválasztunk a körvonalon, akkor a kör $O$ középpontja az $A B C$ háromszög belsejébe esik. Ha az $A$ , $B$ pontok $O$ -ra való tükörképét $A'$ , $B'$ jelöli, akkor ez éppen azt jelenti, hogy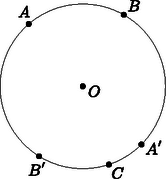
$B \neq A, A'$ és $C$ a (rövidebbik) $A' B'$ ív belső pontja.

Rögzítve egy körüljárási irányt, kölcsönösen egyértelmű megfeleltetést létesíthetünk az összes

(B, C)

pontpárok és a

[0,1) \times [0,1)

egységnégyzet

(b, c)

pontjai között, ahol egy

X

pontra

x

jelöli az irányított

A X

ív hosszát.
Az

A B C

háromszög hegyesszögű voltának megfelelő

(b, c)

pontok halmazát az ábrán bevonalkázott rész szemlélteti, a határpontokat figyelmen kívül hagyva.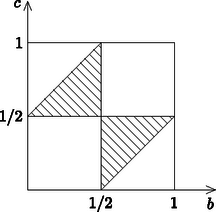

Mivel annak valószínűsége, hogy a

P

pont egy adott

X Y

ívre esik, megegyezik az

X Y

ív hosszával, a

B

C

pontok független választása miatt úgy érvelhetünk, hogy a keresett valószínűség megegyezik a bevonalkázott tartomány területével (pontosabban e területnek a teljes egységnégyzet területéhez való arányával), ami éppen 1/4.

II. megoldás. Használjuk továbbra is az I. megoldás jelöléseit. Az

A

csúcsot tekintsük most is rögzítettnek, továbbá tegyük fel, hogy már a

B

csúcsot is kiválasztottuk; ennek az

A

-tól való ívtávolsága (a rövidebbik

A B

ív hossza) legyen

α

(

0 < α < 1 / 2

). Meghatározzuk az

α

függvényében annak a (feltételes) valószínűségét, hogy a harmadik,

C

pont megválasztásával az

A B C

háromszög hegyesszögű. Mint láttuk, ez pontosan akkor van így, ha

C

a rövidebbik

A' B'

körív belső pontja. Ennek ‐ az

A B

-vel egybevágó ‐ körívnek a hossza ugyancsak

α

, ezért

C

megfelelő választásának valószínűsége

α / 1 = α

. A feladat kérdésére adandó válasz az

α

,,átlaga'' (pontosabban a

(0,1 / 2)

intervallumon értelmezett

α \to α

függvény integrál-közepe az adott intervallumon), ami

(1 / 8) / (1 / 2) = 1 / 4

Megjegyzés. A probléma térbeli változatát a B. 4086. feladatban fogalmaztuk meg. Az ahhoz közölt megoldás magyarázatot ad az eredmények gyanús ,,szabályosságára'' is: a síkbeli

1 / 4 = 1 / 2^{2}

mellett a tetraéderre vonatkozó megfelelő valószínűség

1 / 8 = 1 / 2^{3}

. A térbeli változat bármelyik megoldása igen egyszerűen adaptálható a síkra; az így kapható III. megoldás(ok) megfogalmazását az Olvasóra bízzuk.