Kezdőlap


Feladat:	B.4067	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Welsz Edit , Zsupanek Alexandra
Füzet:	2008/december, 541 - 543. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai bizonyítások, Szinusztétel alkalmazása, Hasonlósági transzformációk, Hossz, kerület, Oldalak aránya és szögek közötti kapcsolat, Háromszögek geometriája, Feladat
Hivatkozás(ok):	Feladatok: 2008/február: B.4067

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. Három esetet kell vizsgálnunk: a hegyesszögű, a derékszögű és a tompaszögű háromszög esetét. Jelöljük az új háromszög csúcsait 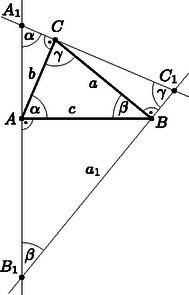$A_{1}$ , $B_{1}$ és $C_{1}$ -gyel.
Az $A_{1} B_{1} C_{1}$ háromszög mindhárom esetben hasonló az eredeti $A B C$ háromszöghöz, mert szögeik egyenlőek (merőleges szárú szögpárok). Legyen a két háromszög hasonlóságának aránya $λ$ .
1. Ha a háromszög hegyesszögű (1. ábra):

\begin{matrix} λ = \frac{B_{1} C_{1}}{B C} = \frac{a_{1}}{a} = \frac{K}{k}, a_{1} = B_{1} B + B C_{1}, \end{matrix}

B C C_{1}

háromszögben

ctg γ = \frac{B C_{1}}{a}

, az

A B B_{1}

háromszögben

sin β = \frac{c}{B B_{1}}

1. ábra

Ezek alapján:

\begin{matrix} \frac{a_{1}}{a} = \frac{B_{1} B}{a} + \frac{B C_{1}}{a} = \frac{c}{a \cdot sin β} + ctg γ . \end{matrix}

A szinusztétel alapján az első tag:

\begin{matrix} \frac{c}{a} \cdot \frac{1}{sin β} & = \frac{sin γ}{sin α} \cdot \frac{1}{sin β} = \frac{sin [180^{\circ} - (α + β)]}{sin α \cdot sin β} = \frac{sin α \cdot cos β + cos α \cdot sin β}{sin α \cdot sin β} = \\ = \frac{cos β}{sin β} + \frac{cos α}{sin α} = ctg β + ctg α, \end{matrix}

vagyis

\begin{matrix} \frac{a_{1}}{a} = ctg α + ctg β + ctg γ = \frac{K}{k} . \end{matrix}

2. Derékszögű háromszögben (2. ábra):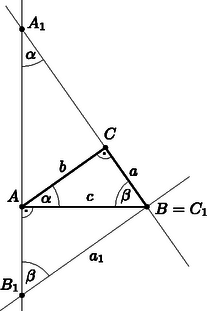

\begin{matrix} λ = \frac{B_{1} C_{1}}{B C} = \frac{a_{1}}{a} = \frac{K}{k}, \end{matrix}

A B B_{1}

háromszögben

\begin{matrix} sin β = \frac{c}{a_{1}}, vagyis \frac{a_{1}}{a} = \frac{c}{a \cdot sin β} . \end{matrix}

2. ábra

Az előző esethez hasonlóan belátható, hogy

\begin{matrix} \frac{c}{a \cdot sin β} = ctg β + ctg α . \end{matrix}

Mivel

γ = 90^{\circ}

, azért

ctg γ = 0

, így

\begin{matrix} \frac{a_{1}}{a} = ctg α + ctg β + ctg γ = \frac{K}{k} . \end{matrix}

3. Tompaszögű háromszögben (3. ábra):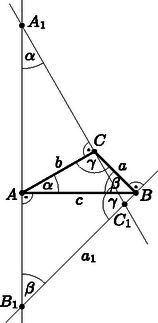

\begin{matrix} λ = \frac{B_{1} C_{1}}{B C} = \frac{a_{1}}{a} = \frac{K}{k}, a_{1} = B_{1} B - B C_{1}, \end{matrix}

A B B_{1}

háromszögben

sin β = \frac{c}{B_{1} B}

, a

B C C_{1}

háromszögben

\begin{matrix} ctg (180^{\circ} - γ) = \frac{B C_{1}}{a} = - ctg γ, \end{matrix}

amiből

\begin{matrix} \frac{a_{1}}{a} = \frac{B_{1} B}{a} - \frac{B C_{1}}{a} = \frac{c}{a \cdot sin β} - ctg (180^{\circ} - γ) . \end{matrix}

Hasonlóan az 1. esethez:

\begin{matrix} \frac{c}{a \cdot sin β} = ctg β + ctg α, \end{matrix}

vagyis összegezve

\begin{matrix} \frac{a_{1}}{a} = ctg α + ctg β + ctg γ = \frac{K}{k} . \end{matrix}

3. ábra

Az állítást mindhárom esetben beláttuk, így az bármely háromszögben igaz.