Kezdőlap


Feladat:	B.4057	Korcsoport: 18-	Nehézségi fok: könnyű
Megoldó(k):	Gaál Alexisz Tamás , Ratku Antal , Wang Daqian
Füzet:	2008/december, 538 - 539. oldal		PDF \| MathML
Témakör(ök):	Magasabb fokú egyenletek, Függvények ábrázolása, Függvényvizsgálat differenciálszámítással, Számtani-mértani egyenlőtlenségek, Feladat
Hivatkozás(ok):	Feladatok: 2008/január: B.4057

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Ábrázoljuk az $f (x) = x^{6} - 6 x + 5$ függvényt számítógépes program segítségével.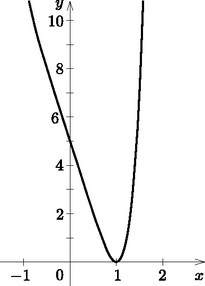
Az ábra alapján sejthető, hogy a függvénynek az $x = 1$ helyen van gyöke, esetleg többszörös gyöke. Nézzük meg a függvény értékét az $x = 1$ helyen: $f (1) = 0$ . Az egyenletnek $x = 1$ valóban gyöke, így a polinomból kiemelhetünk $(x - 1)$ -et:

\begin{matrix} f (x) & = x^{6} - 6 x + 5 = \\ = (x - 1) (x^{5} + x^{4} + x^{3} + x^{2} + x - 5) . \end{matrix}

Ha a második tényezőben

x

helyére

1

-et írunk, ismét 0-t kapunk. Tehát újból kiemelhető

x - 1

\begin{matrix} f (x) = {(x - 1)}^{2} (x^{4} + 2 x^{3} + 3 x^{2} + 4 x + 5) . \end{matrix}

Itt az utolsó tényező már nem ad 0-t az

x = 1

helyen. Az ábra alapján azt sejtjük, hogy több gyök nincs. Ha belátjuk, hogy az utolsó tényező mindig pozitív, akkor azzal bebizonyítjuk, hogy valóban nincs több gyöke az egyenletnek.

x^{4} + 2 x^{3}

hasonlít

x^{2} + x

négyzetére:

{(x^{2} + x)}^{2} = x^{4} + 2 x^{3} + x^{2}

. Marad még

2 x^{2} + 4 x + 5

, amiről könnyen látszik, hogy átalakítható:

\begin{matrix} 2 x^{2} + 4 x + 5 = 2 (x^{2} + 2 x + 1) + 3 = 2 {(x + 1)}^{2} + 3. \end{matrix}

Azt kaptuk, hogy

\begin{matrix} x^{4} + 2 x^{3} + 3 x^{2} + 4 x + 5 = {(x^{2} + x)}^{2} + 2 {(x + 1)}^{2} + 3 \geq 3. \end{matrix}

Ezzel beláttuk, hogy az egyenlet egyetlen gyöke az

x = 1

II. megoldás. Vegyük észre, hogy

x = 1

megoldása az egyenletnek. Megmutatjuk, hogy ez az egyetlen gyök. Vizsgáljuk meg az

f (x) = x^{6} - 6 x + 5

függvény deriváltfüggvényét.

f' (x) = 6 x^{5} - 6

. Ez csak

x = 1

esetén 0. A deriváltfüggvény

x < 1

esetén negatív és

x > 1

esetén pozitív. Tehát

f (x)

szigorúan monoton csökken, ha

x < 1

x = 1

esetén értéke 0, és

x > 1

esetén szigorúan monoton nő. Ebből következik, hogy

f (x) > 0

, ha

x \neq 1

.
Mivel a függvény csak az

x = 1

helyen 0, így a polinomnak ez az egyetlen gyöke.

Megjegyzés. Többen helytelenül ekvivalens állításként értelmezték az első derivált 0 voltát és a szélsőérték létezését, pedig csak az igaz, hogy ha létezik szélsőérték, akkor ott a derivált 0.

III. megoldás. Az egyenletet átrendezve az

x^{6} + 5 = 6 x

egyenlethez jutunk.
Ennek bal oldala

x \leq 0

esetén legalább 5, míg a jobb oldal legfeljebb 0. Ebben az esetben tehát nincs gyöke az egyenletnek.
Osszuk el a kapott egyenlet mindkét oldalát 6-tal. A számtani és mértani közepek között fennálló egyenlőtlenséget felhasználva

x > 0

esetén azt kapjuk, hogy

\begin{matrix} \frac{x^{6} + 5}{6} = \frac{x^{6} + 1 + 1 + 1 + 1 + 1}{6} \geq \sqrt[6]{x^{6} \cdot 1 \cdot 1 \cdot 1 \cdot 1 \cdot 1} = x, \end{matrix}

ahol egyenlőség

x^{6} = 1

, vagyis

x > 0

miatt

x = 1

esetén teljesül.
Az egyenlet egyetlen valós megoldása tehát

x = 1