Kezdőlap


Feladat:	C.918	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Csizmadija Laura
Füzet:	2008/december, 529 - 531. oldal		PDF \| MathML
Témakör(ök):	Téglalapok, Háromszög területe, Szimmetrikus sokszögek, Súlyvonal, Terület, felszín, C gyakorlat
Hivatkozás(ok):	Feladatok: 2007/november: C.918

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Az adott $A B C D$ téglalap területét jelölje $T$ , az oldalak felezőpontjai legyenek $A_{1}$ , $B_{1}$ , $C_{1}$ , $D_{1}$ . A $K$ , $K_{1}$ és $K_{2}$ pontok jelöljék rendre az $A C_{1}$ szakasznak a $B D_{1}$ , $D A_{1}$ és $C D_{1}$ szakaszokkal való metszéspontjait. Hasonlóan képezzük az $L$ , $L_{1}$ , $L_{2}$ , valamint az $M$ , $M_{1}$ , $M_{2}$ , illetve az $N$ , $N_{1}$ , $N_{2}$ pon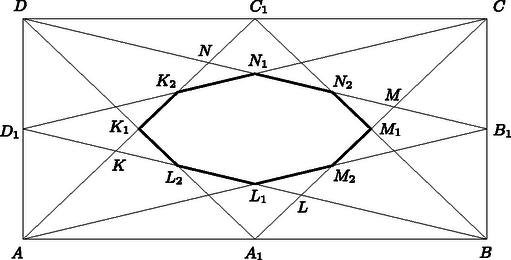tokat.

Szemköztes oldalainak párhuzamossága miatt az

A A_{1} C C_{1}

négyszög paralelogramma, melynek magassága megegyezik az

A B C D

téglalap

A B

oldalához tartozó magasságával, az alapja pedig fele az adott téglalap

A B

alapjának; ezért a paralelogramma területe

\frac{T}{2}

.
Hasonlóan a

K L M N

négyszög ugyancsak paralelogramma. Ennek a paralelogrammának a magassága megegyezik az

A A_{1} C C_{1}

paralelogramma

A_{1} C

és

A C_{1}

oldalai közötti magassággal. Számítsuk ki a paralelogramma

K N

oldalát: a

D_{1} K

M B_{1}

és

C_{1} L

szakaszok az

A N D

C L B

és

D M C

háromszögek középvonalai. Ebből következik, hogy

A K = K N = L M = M C = 2 N C_{1}

. Tudjuk még, hogy

N A D ▵ \sim N C_{1} L_{1} ▵

és így

\begin{matrix} \frac{C_{1} N}{A N} = \frac{C_{1} L_{1}}{A D} = \frac{1}{4}, tehát K N = \frac{2}{5} A C_{1} . \end{matrix}

Ezért a

K L M N

paralelogramma területe

\frac{T}{5}

.
A

K_{1}

pont az

A A_{1} C_{1} D

téglalap átlóinak metszéspontja, ezért

A K_{1} = K_{1} C_{1}

.
A

K_{2}

pont az

A C D

háromszög

A C_{1}

és

C D_{1}

súlyvonalainak a metszéspontja, tehát az

A C D

háromszög súlypontja, ezért

A K_{2} = 2 K_{2} C_{1}

.
Ezekből kapjuk, hogy

\begin{matrix} K K_{1} = A K_{1} - A K = \frac{1}{2} A C_{1} - K N = \frac{5}{4} K N - K N = \frac{1}{4} K N \end{matrix}

és

\begin{matrix} K_{2} N = A N - A K_{2} = 2 K N - \frac{2}{3} A C_{1} = 2 K N - \frac{2}{3} \cdot \frac{5}{2} K N = \frac{1}{3} K N . \end{matrix}

Hasonlóan kapjuk, hogy

K L_{2} = \frac{K L}{3}

. Ezért:

\begin{matrix} T_{K K_{1} L_{2}} & = & \frac{1}{2} K K_{1} \cdot K L_{2} \cdot sin K_{1} K L_{2} ∢ = \frac{1}{2} \cdot \frac{1}{4} K N \cdot \frac{1}{3} \cdot K L \cdot sin N K L ∢ = \\ = & \frac{1}{12} T_{N K L} = \frac{1}{24} T_{K L M N} = \frac{1}{120} T . \end{matrix}

Hasonlóan kapjuk, hogy

T_{L L_{1} M_{2}} = T_{M M_{1} N_{2}} = T_{N N_{1} K_{2}} = \frac{T}{120}

.
Így végül:

\begin{matrix} T_{K_{1} L_{2} L_{1} M_{2} M_{1} N_{2} N_{1} K_{2}} = \frac{1}{5} T - 4 \cdot \frac{1}{120} T = \frac{6 - 1}{30} T = \frac{1}{6} T . \end{matrix}

A kapott nyolcszög területe tehát

\frac{1}{6}

része az eredeti téglalap területének.

II. megoldás. A téglalap két oldalfelező merőlegese (melyeknek metszéspontja

I

) négy egybevágó részre osztja a téglalapot. Elég az egyik ilyen részt megvizsgálni.
Nyilván

B G

felezi az

I F

H C

pedig az

I G

sz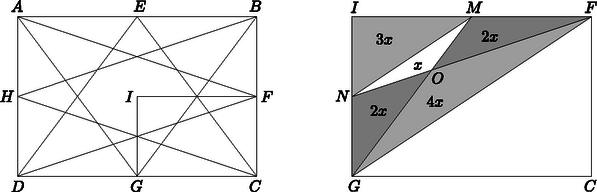akaszt.

I F G

háromszög súlyvonalai harmadolják egymást, és felezik a háromszög területét. Legyen az

O M N ▵

területe

x

. Mivel

2 N O = O F

, azért

2 t_{N O M} = t_{F M O} = 2 x

. Mivel

M N

I N F ▵

súlyvonala, azért

t_{I N M} = t_{O M N} + t_{O F M} = 3 x

. Innen

t_{N G F} = t_{I N F} = 6 x

.
A keresett arány:

\begin{matrix} \frac{3 x + x}{2 \cdot (3 x + x + 2 x + 6 x)} = \frac{4 x}{24 x} = \frac{1}{6} . \end{matrix}

A keletkezett nyolcszög területe hatodrésze a téglalap területének.