Kezdőlap


Feladat:	2008. évi Nemzetközi Fizika Diákolimpia 11. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Füzet:	2008/november, 488 - 492. oldal		PDF \| MathML
Témakör(ök):	Nemzetközi Fizika Diákolimpia, Egyéb merev testek dinamikája
Hivatkozás(ok):	Feladatok: 2008/október: 2008. évi Nemzetközi Fizika Diákolimpia 11. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. A mozsár felépítése
1.1. A $T G$ távolság kiszámítása. A kanálban összegyűlt 1 liter víz forgatónyomatéka egyensúlyt tart az emelőrúd súlyából származó forgatónyomatékkal. Geometriai megfontolásokból kiszámíthatjuk, hogy 1 liter víz esetén a kanálban a vízmagasság 1,2 cm, és ennek a vízmennyiségnek a súlypontja nagyjából 47 cm-re van a $T$ forgástengelytől. Mivel az emelőrúd tömege 30-szor nagyobb 1 liter víz tömegénél, így a kérdéses $T G$ távolság

\begin{matrix} \frac{47}{30} cm = 1, 57 cm \approx 1, 6 cm . \end{matrix}

1.2. Az

α_{1}

és

α_{2}

értékek kiszámítása. Amikor az emelőrúd

α_{1}

dőlésszögénél a víz eléri a kanál peremét, akkor az 1. ábrán látható helyzetet veszi fel. Ekkor a kanálban lévő 1 liter víz egy háromszög alapú egyenes hasábot tölt ki, melynek térfogatát könnyen felírhatjuk:

V = \frac{h b (P Q)}{2} = 1

liter, ahol

b = 15

cm a kanál szélessége. A számítás

P Q \approx 11, 1

cm eredményre vezet.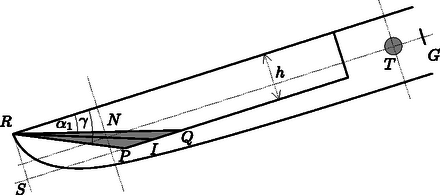

1. ábra

Az emelőrúd

α_{1}

dőlésszögét így számíthatjuk ki:

\begin{matrix} tg α_{1} = \frac{h}{S Q} = \frac{h}{P Q + \sqrt[]{3} h}, \end{matrix}

amiből

α_{1} = 20, 6^{\circ}

.
A kanálból akkor távozik az összes víz, ha az emelőrúd dőlésszöge:

α_{2} = γ = 30^{\circ}

.
1.3. A nulla forgatónyomatékhoz tartozó

β

szög és

m_{1}

víztömeg kiszámítása. Használjuk újra az előző ábrát, és ahol csak lehet, írjuk be a képletekbe a numerikus értékeket. Jelöljük a

P Q

távolságot

x

-szel, amit mérjünk méterben:

P Q = x

(m), amivel így adhatjuk meg a kanálban maradó víz

m

tömegét kilogrammban:

m = ϱ_{víz} \frac{x h b}{2} = 9 x

(kg). A víz súlypontja a

P Q R

háromszög súlypontjában van, az

R I

súlyvonal

2 / 3

részénél. A szerkezet geometriai elrendezéséből következik, hogy az emelőrúd

G

súlypontja, a

T

forgástengely (középpontja) és a kanálban maradó víz

N

súlypontja egy egyenes mentén helyezkedik el. A forgatónyomaték egyensúlyt így írhatjuk fel:

\begin{matrix} m g \cdot T N = M g \cdot T G \Rightarrow m \cdot T N = M \cdot T G = 30 \cdot 0, 0157 = 0, 471 (kgm). \end{matrix}

T N

távolságot így írhatjuk fel:

\begin{matrix} T N = L + a - \frac{2}{3} (\sqrt[]{3} h + \frac{x}{2}) = 0, 94 - 0, 08 \sqrt[]{3} - \frac{x}{3} = 0, 801 - \frac{x}{3} . \end{matrix}

Az eddig meghatározott három kifejezésből (

m = 9 x

;

T N = 0, 801 - \frac{x}{3}

;

m \cdot T N = 0, 471

) a következő másodfokú egyenletre juthatunk:

3 x^{2} - 7, 21 + 0, 471 = 0

, melynek számunkra értelmes gyöke:

x = 0, 0672

. Így a kérdéses tömeg:

m = 9 x = 0, 605

kg, továbbá a dőlési szöget így határozhatjuk meg:

\begin{matrix} tg β = \frac{h}{x + \sqrt[]{3} h} = 0, 436, amiből β = 23, 6^{\circ} . \end{matrix}

2. A rendes munkavégző körfolyamat mennyiségei
2.1. A

μ (α)

forgatónyomaték függvény ábrázolása az

α

szög függvényében. Kezdetben (

α = 0

) nincs víz a kanálban. Ekkor az emelőrúdra ható forgatónyomaték:

\begin{matrix} M g \cdot T G = 30 \cdot 9, 81 \cdot 0, 0157 = 4, 62 Nm \approx 4, 6 Nm. \end{matrix}

Tekintsük ezt a forgatónyomatékot negatív előjelűnek, a negatív forgatónyomaték a rúd dőlésszögét csökkenteni igyekszik. Amikor lassan víz folyik a kanálba, az eredő forgatónyomaték növekedni kezd egészen addig, amíg kissé pozitívvé válik, és a mozsártörő emelkedni kezd. Ezt követően azzal a közelítéssel dolgozunk, hogy a kanálban lévő víz mennyisége nem változik.
Miközben a kanál lefelé billen, a benne lévő víz tömegközéppontja fokozatosan eltávolodik a forgástengelytől, így

μ

egészen addig növekszik, amíg a víz eléri a kanál peremét. Tehát a maximális forgatónyomaték az

α = α_{1} = 20, 6^{\circ}

-os dőlésszögnél jön létre. Az előző részben már megismert számoláshoz hasonlóan kiszámíthatjuk, hogy

μ_{{max}_{}^{}} \approx 2, 7

Nm.
A rúd további dőlése közben a víz elkezd kifolyni a kanálból, és

α = β

esetén

μ = 0

-vá válik. A tehetetlenség következtében

α

tovább növekszik, miközben

μ

csökken.

α = 30^{\circ}

esetén a kanál teljesen kiürül. Ebben a helyzetben a forgatónyomaték:

μ = - M g \cdot T G \cdot cos 30^{\circ} = - 4, 0

Nm. Ezután a tehetetlenség következtében a szög még tovább nő, egészen

α = α_{0}

értékig, amikor a forgatónyomaték:

μ = - M g \cdot T G \cdot cos α_{0} = - 4, 6 \cdot cos α_{0}

Nm. Végül a dőlésszög hirtelen nullára csökken (a mozsártörő lecsap), és a körfolyamat

μ = - 4, 6

Nm értékkel újra kezdődik.
A fentiek alapján felvázolhatjuk a

μ (α)

forgatónyomatékot az

α

szög függvényében (2. ábra):
2.2. A mozsártörő munkavégzésének grafikus értelmezése. A

μ (α)

forgatónyomaték által végzett

W_{teljes}

teljes munkavégzést a forgatónyomaték előjeles görbe alatti területeként számíthatjuk ki a teljes

O A B C D F O

körfolyamatra. A mozsártörőnek átadott

W_{ütés}

energiát az

α_{0}

-tól 0-ig tekintett görbe alatti terület mérőszámaként kaphatjuk meg (

E D F O E

), melynek nagysága: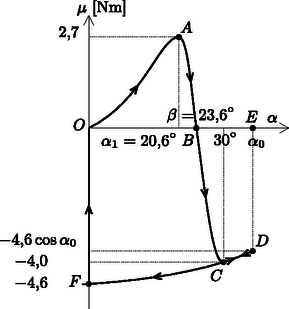

\begin{matrix} M g \cdot T G \cdot sin α_{0} = 4, 6 J \cdot sin α_{0} . \end{matrix}

2. ábra

2.3. Az

α_{0}

szög és

W_{ütés}

becslése. Az

α_{0}

szög értékét abból becsülhetjük meg, hogy ebben a pozícióban az emelőrúd energiája nulla, vagyis az

O A B O

terület megegyezik a

B E D C B

terület nagyságával. Ha az

O A B O

területet háromszöggel, a

B E D C B

területet pedig trapézzal közelítjük, akkor az

α_{0}

szög értékére közelítőleg

35^{\circ}

-ot kapunk. Így a mozsártörő által végzett munka:

\begin{matrix} W_{ütés} = Mg \cdot T G \cdot sin α_{0} = 4, 6 J \cdot sin 35^{\circ} \approx 2, 6 J. \end{matrix}

3. A mozdulatlan állapot
3.1. Az emelőrúd mozgása az

α = β

egyensúlyi helyzet közelében.
3.1.1. Az

α = β

egyensúlyi helyzet közelében a forgatónyomaték nagyjából a 3. ábrán látható módon változik. A grafikon alapján megállapíthatjuk, hogy az egyensúlyi helyzet stabil.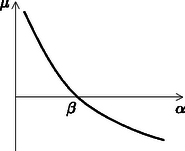

3. ábra

3.1.2. Az

α

szögben megdőlt rúd esetén a kanálban lévő víz tömege:

\begin{matrix} m = \frac{ϱ b h \cdot P Q}{2}, ahol P Q = h (\frac{1}{tg α} - \frac{1}{tg 30^{\circ}}) . \end{matrix}

Miközben a rúd hajlásszöge

β

-ról (

β + Δ α

) értékre változik, a kanálban lévő víz tömegének megváltozása közelítőleg:

\begin{matrix} Δ m = - \frac{b h^{2} ϱ}{2 sin^{2} α} Δ α \approx - \frac{b h^{2} ϱ}{2 sin^{2} β} Δ α . \end{matrix}

A (

β + Δ α

) dőlésszögű rúdra ható

μ

forgatónyomaték megegyezik a

Δ m

tömegből származó nyomatékkal:

\begin{matrix} μ = Δ m g \cdot T N \cdot cos (β + Δ α) . \end{matrix}

T N

távolságot a rúd

β

szöghöz tartozó egyensúlyi állapotából határozhatjuk meg:

\begin{matrix} T N = \frac{M \cdot T G}{m} = \frac{30 \cdot 0, 0157}{0, 605} = 0, 779 m. \end{matrix}

Végül a forgatónyomatékra közelítőleg ezt a numerikus kifejezést kapjuk:

μ \approx - 47 \cdot Δ α

(Nm).
3.1.3. Alkalmazzuk a rúd mozgására a forgómozgás dinamikai alapegyenletét (

μ = I \frac{d^{2} α}{d t^{2}}

, ahol

α = β + Δ α

), melyben az

I

tehetetlenségi nyomaték nem csupán a rúdtól, hanem a kanálban lévő víz tömegétől is függ. Tegyük fel, hogy kicsiny

Δ α

szögek esetén a kanálban lévő víz tömege állandó (

\approx 0, 6

kg) és ezt a vízmennyiséget tekintsük tömegpontnak. A számítás a rendszer tehetetlenségi nyomatékára közelítőleg

I \approx 12, 4 kgm^{2}

-et ad. Így a mozgásegyenlet numerikus alakja (SI egységrendszerben):

\begin{matrix} - 47 \cdot Δ α = 12, 4 \frac{d^{2} Δ α}{d t^{2}}, \end{matrix}

ami egy harmonikus rezgőmozgás egyenlete. A mozgás rezgésideje:

\begin{matrix} τ = 2 π \sqrt[]{\frac{12, 4}{47}} \approx 3, 2 s. \end{matrix}

3.2. A vízhozam számítása kis amplitúdójú rezgés esetén. Az emelőrúd szögkitérésének időfüggését így írhatjuk fel az egyensúlyi helyzet körül:

\begin{matrix} Δ α = - Δ α_{0} sin (\frac{2 π t}{τ}), ahol Δ α_{0} = 1^{\circ} . \end{matrix}

Ilyenkor a rúd a

t = 0

kezdőpillanat után a kisebb szögkitérések felé indul el, és ott nagyobb vízmennyiségre van szükség a túlfolyás elérésére. Rövid

d t

idő alatt a rúd lehajlása

d α

szöggel változik meg:

\begin{matrix} d (Δ α) = d α = - Δ α_{0} \frac{2 π}{τ} cos (\frac{2 π t}{τ}) \cdot d t . \end{matrix}

A túlfolyáshoz ennyi idő alatt legalább a következő mennyiségű víznek kell a kanálba csorognia:

\begin{matrix} d m = - \frac{b h^{2} ϱ}{2 sin^{2} β} d α = \frac{2 π Δ α_{0} b h^{2} ϱ d t}{2 τ sin^{2} β} cos (\frac{2 π t}{τ}) . \end{matrix}

Ennek maximuma

t = 0

-nál van, vagyis a túlfolyás akkor lesz folyamatos, ha a vízhozamra (

d m = Φ d t

) teljesül, hogy

\begin{matrix} Φ \geq Φ_{1} = \frac{π b h^{2} ϱ}{τ sin β} Δ α_{0} = \frac{π b h^{2} ϱ}{τ sin β} \cdot \frac{2 π}{360} \approx 0, 23 kg/s, \end{matrix}

ahol a rezgés

1^{\circ}

-os szögamplitúdóját

\frac{2 π}{360}

radián alakban írtuk fel.
3.3. Mekkora minimális vízhozam esetén nem működik a mozsár? Ha a kanál eléri a

20, 6^{\circ}

-os dőlési szöget, miközben mindvégig túlcsordul, akkor benne 1 kg víz lesz, és a rezgési amplitúdója

23, 6^{\circ} - 20, 6^{\circ} = 3^{\circ}

-os lesz. Eltekintve a rendszer tehetetlenségi nyomatékának változásától (amit a növekvő vízmennyiség okoz), a háromszoros amplitúdó háromszoros vízhozamot is jelent:

Φ_{2} = 3 Φ_{1} \approx 0, 7

kg/s. Ennél nagyobb vízhozam esetén a rizshántoló mozsár nem tud működni.