| Feladat: | B.4076 | Korcsoport: 16-17 | Nehézségi fok: könnyű |
| Megoldó(k): | Fonyó Dávid | ||
| Füzet: | 2008/november, 476 - 478. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Konstruktív megoldási módszer, Háromszög területe, Többszemélyes véges játékok, Feladat | ||
| Hivatkozás(ok): | Feladatok: 2008/március: B.4076 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Megoldás. Ha Nóra az vagy pontot választaná, akkor Kristóf a pontot a , illetve ponthoz elegendően közel választva elérheti, hogy háromszög területe 0-hoz tetszőlegesen közel legyen, attól függetlenül, hogy Nóra hol jelöli ki oldalon az pontot. 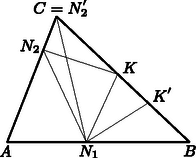 Ha Kristóf a oldalon olyan pontot választana, melyre , akkor például Nóra választása esetén 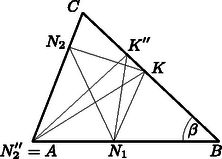 (Az ábrán hegyesszög, de a fenti megállapítások és esetén is érvényesek.) Így beláttuk, hogy Kristófnak mindenképpen úgy kell megválasztani a oldalon a pontot, hogy legyen, és ekkor a Nóra által a oldalon megadott ponttól már független az háromszög területe. Tehát a helyes játékstratégia esetén jó megválasztásától függ az háromszög területének maximuma. miatt és hasonló, mivel és (3. ábra). Mivel , a korábban megállapított hasonlóság alapján , és az -ben a csúcshoz tartozó magasság hossza . Így az és az párhuzamos oldalak távolsága , ezért az háromszög területe: 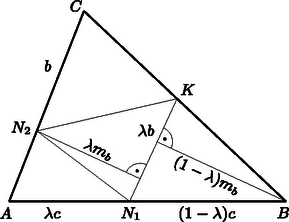 Tehát a helyes játékstratégia esetén: ‐ Nóra az oldal felezőpontját választja -nek; ‐ Kristóf a oldal felezőpontját választja -nak ( középvonal ); ‐ Végül Nóra tetszőleges pontot jelöl ki az oldalon. Így az háromszög területe az háromszög területének -ed része. |