| Feladat: | B.4059 | Korcsoport: 18- | Nehézségi fok: nehéz |
| Megoldó(k): | Aczél Gergely , Bálint Dániel , Blázsik Zoltán , Bodor Bertalan , Dinh Hoangthanh Attila , Énekes Péter , Kalina Kende , Keresztfalvi Tibor , Kiss Eszter , Kovács Noémi , Márkus Bence , Mezei Márk , Misnyovszki Péter , Perjési Gábor , Tóth Bence Barnabás , Tóth László Márton , Tubak Dániel , Varga László , Wang Daqian , Zieger Milán | ||
| Füzet: | 2008/november, 475 - 476. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Síkgeometriai szerkesztések, Konstruktív megoldási módszer, Egybevágósági transzformációk, Feladat | ||
| Hivatkozás(ok): | Feladatok: 2008/január: B.4059 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. megoldás. Vegyük fel úgy az -ból induló , , félegyeneseket, hogy és ne essenek egybe, de mindkettő derékszöget zárjon be az félegyenessel. Az félegyenesen jelöljük ki az , pontokat úgy, hogy legyen. A rövidség kedvéért nevezzünk két síkidomot -ekvivalensnek, ha minden középpontú körnek ugyanakkora területű részét tartalmazzák. Az alábbi konstrukció két egyszerű észrevételen alapszik: 1. Ha a sokszöget olyan egybevágósági transzformáció viszi -be, amelynél az pont fixen marad, akkor biztosan -ekvivalens -vel. (A transzformáció ugyanis minden középpontú kört önmagára képez, ezért és közös részének a képe és közös része lesz.) 2. Ha és valamint és egymással -ekvivalens, továbbá -nak és -nek, illetve -nek és -nek nincs közös belső pontja, akkor és egyesítése -ekvivalens és egyesítésével. 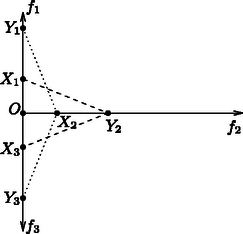 Az és az háromszögek -ekvivalensek, mivel az derékszög belső felezőjére való tükrözés egymásba viszi őket, és ennek során az pont fix. Hasonlóan és is -ekvivalensek. A második észtevételünk szerint így az és az összetételével adódó háromszög is -ekvivalens az és az összetételével adódó háromszöggel. Végül, e két háromszög egyenlő szárú, mivel az és oldalukhoz tartozó közös magasság-egyenesük mindkét oldalt felezi. A két alap , tehát a két háromszög nem egybevágó. 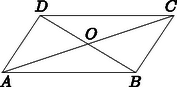 |