Kezdőlap


Feladat:	2008. évi Nemzetközi Matematika Diákolimpia 23. feladata	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Tomon István
Füzet:	2008/október, 393 - 394. oldal		PDF \| MathML
Témakör(ök):	Körérintési szerkesztések, Beírt kör, Konvex négyszögek, Síkgeometriai bizonyítások, Nemzetközi Matematikai Diákolimpia
Hivatkozás(ok):	Feladatok: 2008/szeptember: 2008. évi Nemzetközi Matematika Diákolimpia 23. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Tomon István megoldása. Lemma: Ha egy $A B C D$ négyszögnél létezik az $ω$ kör, akkor

\begin{matrix} A B + A D = C B + C D . \end{matrix}

Bizonyítás: Legyenek az

ω

kör érintési pontjai az oldalegyenesekkel az ábrán látható módon

T_{1}

T_{2}

T_{3}

T_{4}

. Ekkor felhasználva, hogy egy adott pontból a körhöz húzott érintőknek hossza megegyezik, azt kapjuk, hogy

\begin{matrix} B T_{4} = B T_{1} . \end{matrix}

(1)

Ezen kívül a következő egyenlőséglánc teljesül:

\begin{matrix} B T_{4} & = B C + C T_{4} = B C + C T_{2} = B C + C D + D T_{2} = B C + C D + D T_{3} = \\ = B C + C D + A T_{3} - A D = B C + C D + A T_{1} - A D = \\ = B C + C D + B T_{1} - A D - A B . \end{matrix}

Ezt összevetve (1)-gyel azt kapjuk, hogy

B C + C D = A B + A D

, s ezzel a Lemmát bebizonyítottuk.

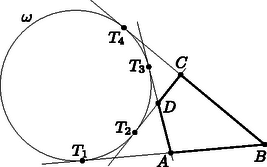Most térjünk rá a feladat bizonyítására. Húzzuk meg az

ω_{1}

kör

A C

-től különböző,

A C

-vel párhuzamos érintőjét, érintse ez

ω_{1}

-et az

E'

pontban.

ω_{1}

és

A C

érintési pontja legyen

E

ω_{2}

és

A C

érintési pontja

F

, ezen kívül húzzuk meg az

ω

körnek az

A C

-vel párhuzamos érintőjét, amely elválasztja

B

-t

ω

-tól, érintse ez

ω

-t a

H

pontban.
Az ismert összefüggés alapján

C E = \frac{- A B + B C + C A}{2}

és

A F = \frac{- C D + A D + A C}{2}

, tehát a Lemma alapján

C E = A F

. Ez azt jelenti, hogy

F

A B C

háromszög

A C

oldalához írt körnek az érintési pontja, tehát ha az

A C

-vel

E'

-n át húzott egyenest

B

-ből

A C

-be nyújtjuk, akkor

E'

F

-be kerül, így

B

E'

F

egy egyenesen vannak, tehát

B

E'

F

H

egy egyenesen vannak.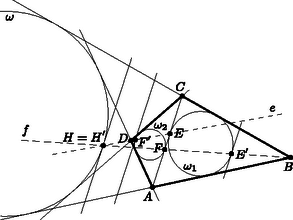

Legyen

H'

ω_{1}

és

ω_{2}

közös külső érintőinek metszéspontja. Ekkor a

H'

-ből az

ω_{2}

-t az

ω_{1}

körbe nagyíthatjuk, s ekkor az

F

pont az

E'

pontba megy át, így

H'

F

E'

egy egyenesen vannak. Vagyis

B

E'

F

H

H'

egy egyenesen vannak, azaz nézzük csak azt, hogy

B

F

H

H'

egy

f

egyenesen vannak. Hasonlóan, ha

D

-t tekintjük a nyújtás középpontjának, akkor

H

D

F'

E

egy egyenesen vannak. Tekintsük újra a

H'

-ből az

ω_{2}

nagyítását

ω_{1}

-be. Ekkor az

F'

pont

E

-be megy át, így

H'

F'

E

egy egyenesen vannak. Tehát

H'

H

D

E

egy

e

egyenesen vannak. A

B A \neq B C

feltétel biztosítja, hogy a

B F

egyenes nem azonos a

D E

egyenessel. Ezért az

e

és az

f

egyenesek különbözők, tehát csak egyetlen közös pontjuk van. Így szükségképpen

H = H'

, s mivel

H

rajta van a körön, így

H'

is, s ezzel az állítást bebizonyítottuk.