Kezdőlap


Feladat:	2008. évi Nemzetközi Matematika Diákolimpia 11. feladata	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Kornis Kristóf
Füzet:	2008/október, 388. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai bizonyítások, Oldalfelező merőleges, Magasságpont, Körülírt kör, Hatványvonal, hatványpont, Nemzetközi Matematikai Diákolimpia
Hivatkozás(ok):	Feladatok: 2008/szeptember: 2008. évi Nemzetközi Matematika Diákolimpia 11. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Kornis Kristóf megoldása. Legyenek rendre $k_{a}$ , $k_{b}$ , $k_{c}$ az $A_{1} A_{2}$ , $B_{1} B_{2}$ , $C_{1} C_{2}$ átmérőjű körök; $F_{A B}$ , $F_{B C}$ , $F_{C A}$ rendre az $A B$ , $B C$ , $C A$ szakaszok felezőpontjai. Két kör hatványvonala nyilvánvalóan merőleges a középpontjaikat összekötő egyenesre. Emiatt $k_{a}$ és $k_{b}$ hatványvonala, és $C H$ is merőleges $F_{B C} F_{A C}$ -re, de mivel mindkettőnek eleme $H$ , e két egyenes egybeesik, azaz a $C$ pontnak a $k_{a}$ és $k_{b}$ körökre vonatkozó hatványa megegyezik. Vagyis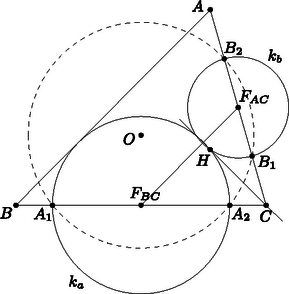

\begin{matrix} C A_{1} \cdot C A_{2} = C B_{1} \cdot C B_{2} . \end{matrix}

Azaz

A_{1}

A_{2}

B_{1}

B_{2}

egy körön fekszenek, melynek középpontja az

A_{1} A_{2}

és a

B_{1} B_{2}

szakaszok felezőmerőlegeseinek metszéspontja. Ezek a felezőmerőlegesek viszont éppen egybeesnek az oldalfelező merőlegesekkel, azaz az

A_{1} A_{2} B_{1} B_{2}

kör középpontja

O

, ha

O

a körülírt kör középpontja, tehát

\begin{matrix} O A_{1} = O A_{2} = O B_{1} = O B_{2} . \end{matrix}

Hasonlóan bizonyíthatjuk, hogy

\begin{matrix} O A_{1} & = O A_{2} = O C_{1} = O C_{2} \Rightarrow \\ \Rightarrow O A_{1} & = O A_{2} = O B_{1} = O B_{2} = \\ = O C_{1} = O C_{2} . \end{matrix}