Kezdőlap


Feladat:	B.4085	Korcsoport: 16-17	Nehézségi fok: könnyű
Megoldó(k):	Dudás Zsolt , Márki Róbert , Zsupanek Alexandra
Füzet:	2008/szeptember, 344 - 345. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai bizonyítások, Érintőnégyszögek, Trapézok, Húrnégyszögek, Terület, felszín, Derékszögű háromszögek geometriája, Feladat
Hivatkozás(ok):	Feladatok: 2008/április: B.4085

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Az $A B C D$ egyenlő szárú trapéz beírt körének középpontja legyen $O$ , az $A B$ száron lévő érintési pont $T$ , az érintőszakaszokat pedig jelölje 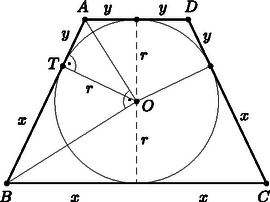$x$ és $y$ . Ekkor $2 \cdot O A T ∢ + 2 \cdot O B T ∢ = 180^{\circ}$ , amiből $O A T ∢ + O B T ∢ = 90^{\circ}$ és így $A O B ∢ = 90^{\circ}$ .

A O B

derékszögű háromszögben az átfogóhoz tartozó magasság

r

, a beírt kör sugara. Alkalmazva a magasság tételt:

r^{2} = x \cdot y

; ezt 4-gyel szorozva:

{(2 r)}^{2} = 2 x \cdot 2 y

vagyis

2 r = \sqrt[]{2 x \cdot 2 y}

, ahol

2 r

a trapéz magassága,

2 x

illetve

2 y

pedig az alapok hossza. Tehát a trapéz magassága mértani közepe az alapoknak.

II. megoldás. A trapéz alapjai legyenek

a

és

c

, szárai pedig

b

hosszúak. A szimmetrikus trapéz mindenképpen húrnégyszög, így fel lehet rá írni a húrnégyszögekre vonatkozó területképletet:

\begin{matrix} T = \sqrt[]{(s - a) (s - b) (s - c) (s - d)} = \sqrt[]{(s - a) {(s - b)}^{2} (s - c)}, \end{matrix}

ahol

s

a fél kerület.
Az érintőnégyszögekre vonatkozó területképlet alapján:

T = s \cdot r = s \cdot \frac{m}{2}

, hiszen a trapéz magassága

m = 2 r

.
Az érintőnégyszög szemközti oldalainak összege egyenlő, tehát

s = a + c = 2 b

. Emiatt

s - a = c

s - b = b

és

s - c = a

. Ezek alapján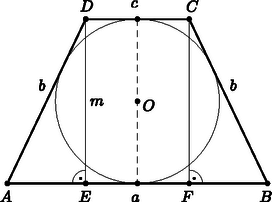

\begin{matrix} T = s \cdot \frac{m}{2} = \sqrt[]{c b^{2} a} = b \sqrt[]{a c}, \end{matrix}

amibe

s = 2 b

-t beírva:

m = \sqrt[]{a c}

III. megoldás. Mivel a négyszög érintőnégyszög, szemközti oldalainak összege megegyezik:

a + c = b + d

, és mivel szimmetrikus a trapéz, azért

b = d

Vagyis

a + c = 2 b

, amiből

\begin{matrix} A D = b = \frac{a + c}{2} . \end{matrix}

D

és

C

csúcsokból állítsunk merőlegeseket az

A B

alapra, a talppontokat jelölje

E

és

F

. Ekkor

A E = B F = \frac{a - c}{2}

.
Az

A E D

háromszögre felírva a Pitagorasz-tételt:

A D^{2} = A E^{2} + D E^{2}

, vagyis

\begin{matrix} {(\frac{a + c}{2})}^{2} = {(\frac{a - c}{2})}^{2} + m^{2}, azaz \frac{a^{2} + 2 a c + c^{2}}{4} = \frac{a^{2} - 2 a c + c^{2}}{4} + m^{2}, \end{matrix}

ahonnan

m^{2} = a c

, tehát

m = \sqrt[]{a c}