Kezdőlap


Feladat:	B.4048	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Éles András , Kukoda Balázs
Füzet:	2008/szeptember, 341 - 343. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai bizonyítások, Szabályos sokszögek geometriája, Trigonometriai azonosságok, Alakzatok köré írt kör, Húrnégyszögek, Pitagorasz-tétel alkalmazásai, Feladat
Hivatkozás(ok):	Feladatok: 2007/december: B.4048

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A szabályos $2 n$ oldalú sokszög köré kör írható. Az ábra alapján meghatározhatjuk a szükséges szögeket: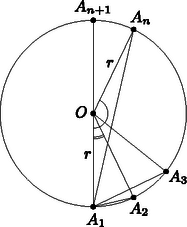

\begin{matrix} A_{1} O A_{2} & = & \frac{360^{\circ}}{2 n} = \frac{180^{\circ}}{n}, \\ A_{1} O A_{3} & = & \frac{360^{\circ}}{n}, \\ A_{1} O A_{n} & = & \frac{(n - 1) \cdot 360^{\circ}}{2 n} = \frac{(n - 1) \cdot 180^{\circ}}{n} . \end{matrix}

O A_{1} A_{2}

egyenlő szárú háromszögből:

\begin{matrix} A_{1} A_{2} = 2 r \cdot sin \frac{90^{\circ}}{n} . \end{matrix}

O A_{1} A_{3}

egyenlőszárú háromszögből:

A_{1} A_{3} = 2 r \cdot sin \frac{180^{\circ}}{n}

. Az

O A_{1} A_{n}

egyenlőszárú háromszögből pedig:

\begin{matrix} A_{1} A_{n} & = & 2 r \cdot sin \frac{(n - 1) \cdot 90^{\circ}}{n} = 2 r \cdot sin [(1 - \frac{1}{n}) \cdot 90^{\circ}] = \\ = & 2 r \cdot sin [90^{\circ} - \frac{90^{\circ}}{n}] = 2 r \cdot cos \frac{90^{\circ}}{n} . \end{matrix}

α = \frac{90^{\circ}}{n}

jelölést bevezetve, a feladat állítása:

\begin{matrix} \frac{1}{4 r^{2} sin^{2} α} + \frac{1}{4 r^{2} cos^{2} α} = \frac{4}{4 r^{2} sin^{2} 2 α} . \end{matrix}

Mindkét oldalt

4 r^{2}

-el szorozva:

\begin{matrix} \frac{1}{sin^{2} α} + \frac{1}{cos^{2} α} = \frac{4}{sin^{2} 2 α} . \end{matrix}

Közös nevezőre hozva és felhasználva, hogy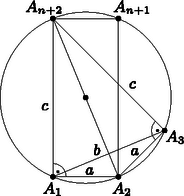

sin 2 α = 2 sin α \cdot cos α

\begin{matrix} \frac{sin^{2} α + cos^{2} α}{sin^{2} α \cdot cos^{2} α} = \frac{4}{4 sin^{2} α \cdot cos^{2} α}, \end{matrix}

és mivel

sin^{2} α + cos^{2} α = 1

, azért

\begin{matrix} \frac{1}{sin^{2} α \cdot cos^{2} α} = \frac{1}{sin^{2} α \cdot cos^{2} α} . \end{matrix}

Mivel ez a bizonyítandó összefüggéssel ekvivalens, az állítást beláttuk.

II. megoldás. Egy

2 n

oldalú szabályos sokszögnek az

A_{1}

csúcsával szemközt az

A_{n + 1}

, az

A_{2}

-vel szemben pedig az

A_{n + 2}

csúcsa van. Ezért

A_{1} A_{2} ∥ A_{n + 1} A_{n + 2}

és

A_{1} A_{2} = A_{n + 1} A_{n + 2}

miatt

A_{1} A_{n + 2} ∥ A_{2} A_{n + 1}

és

A_{1} A_{n + 2} = A_{2} A_{n + 1}

A szabályos sokszög forgásszimmetriája miatt

A_{1} A_{n} = A_{2} A_{n + 1}

, valamint tengelyes tükrössége miatt

A_{1} A_{n + 2} = A_{3} A_{n + 2}

(az

A_{2} A_{n + 2}

szimmetria-tengely szerint). Legyen

A_{1} A_{2} = A_{2} A_{3} = A_{n + 1} A_{n + 2} = a

A_{1} A_{3} = b

A_{1} A_{n + 2} = A_{2} A_{n + 1} = A_{3} A_{n + 2} = c

.
A feladat bizonyítandó állítása:

\begin{matrix} \frac{1}{a^{2}} + \frac{1}{c^{2}} = \frac{4}{b^{2}} . \end{matrix}

A szabályos sokszög köré kör írható, ennek átmérője

A_{2} A_{n + 2}

, így

\begin{matrix} A_{2} A_{1} A_{n + 2} ∢ = 90^{\circ}, \end{matrix}

és mivel

A_{1} A_{2} A_{n + 1} A_{n + 2}

paralelogramma, így téglalap is. Felírhatjuk Ptolemaiosz tételét az

A_{1} A_{2} A_{3} A_{n + 2}

húrnégyszögre:

\begin{matrix} a c + a c = b \cdot A_{2} A_{n + 2}, \end{matrix}

vagyis

2 a c = b \cdot A_{2} A_{n + 2}

, amit négyzetre emelve:

\begin{matrix} 4 a^{2} c^{2} = b^{2} \cdot {(A_{2} A_{n + 2})}^{2} . \end{matrix}

Írjuk föl a Pitagorasz-tételt az

A_{1} A_{2} A_{n + 2}

háromszögre:

{(A_{2} A_{n + 2})}^{2} = a^{2} + c^{2}

. Behelyettesítés és rendezés után:

4 a^{2} c^{2} = b^{2} \cdot (a^{2} + c^{2})

\begin{matrix} \frac{4}{b^{2}} = \frac{a^{2} + c^{2}}{a^{2} c^{2}} = \frac{1}{a^{2}} + \frac{1}{c^{2}} . \end{matrix}

Ezzel az állítást igazoltuk.