Kezdőlap


Feladat:	B.4038	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Csere Kálmán , Énekes Péter
Füzet:	2008/szeptember, 337 - 338. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai bizonyítások, Háromszögek geometriája, Oldalfelező merőleges, Középvonal, Vektorok felbontása összetevőkre, Középpontos tükrözés, Feladat
Hivatkozás(ok):	Feladatok: 2007/november: B.4038

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Az $A B$ , $B C$ és $A C$ oldalak felezőpontjai legyenek $E$ , $F$ és $G$ . Mivel $G F$ középvonal az $A B C$ háromszögben, azért $A B = 2 \cdot G F$ és $A B$ párhuzamos $G F$ -fel. Valamint $G F$ középvonal az $A' B' P$ háromszögben is, ezért $A' B' = 2 \cdot G F$ és $A' B'$ párhuzamos $G F$ -fel. Így $A B$ párhuzamos és egyenlő $A' B'$ -vel, tehát $A B A' B'$ paralelogramma, és átlói, $A A'$ és $B B'$ , felezik egymást.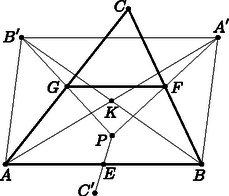

Hasonlóan belátható, hogy az

A C A' C'

négyszög is paralelogramma és átlói,

A A'

és

C C'

is felezik egymást. Tehát az

A A'

B B'

C C'

egyenesek egy ponton mennek át, a közös

K

felezőpontjukon.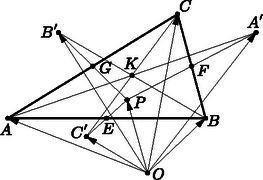

II. megoldás. Tetszőleges

O

vonatkoztatási pontból az

A

A'

B

B'

C

C'

és

P

pontokba mutató vektorok legyenek rendre

a

a'

b

b'

c

c'

és

p

A B

B C

és

A C

oldalak felezőpontjait jelölje

E

F

és

G

.
A tükrözés miatt ezek a pontok egyben a

P C'

P A'

és

P B'

szakaszok felezőpontjai is. Vagyis

\begin{matrix} \vec{O E} = \frac{a + b}{2} = \frac{p + c'}{2}, \vec{O F} = \frac{b + c}{2} = \frac{p + a'}{2}, \vec{O G} = \frac{a + c}{2} = \frac{p + b'}{2} . \end{matrix}

Ezekből kifejezhetjük az

a'

b'

c'

vektorokat:

\begin{matrix} c' = a + b - p, a' = b + c - p, b' = a + c - p . \end{matrix}

Ezután állítsuk elő az

A A'

B B'

és

C C'

szakaszok felezőpontjaiba mutató vektorokat:

\begin{matrix} \frac{a + a'}{2} = \frac{a + b + c - p}{2}, \frac{b + b'}{2} = \frac{b + a + c - p}{2}, \frac{c + c'}{2} = \frac{c + a + b - p}{2} . \end{matrix}

Ezek ugyanabba a pontba mutatnak, vagyis a három szakasznak közös a felezőpontja, tehát az egyenesek valóban egy ponton mennek át.