Feladat: B.4034 Korcsoport: 16-17 Nehézségi fok: könnyű
Megoldó(k):  Gyurcsik Judit 
Füzet: 2008/szeptember, 335 - 337. oldal  PDF  |  MathML 
Témakör(ök): Síkgeometriai bizonyítások, Háromszög területe, Számtani sorozat, Párhuzamos szelők tétele és megfordítása, Feladat
Hivatkozás(ok):Feladatok: 2007/november: B.4034

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Az ABC háromszög területét jelölje T. Fejezzük ki T, x és n segítségével az NxFH1 háromszögek és az NxFH2 háromszögek területét, ahol 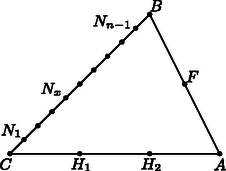x∈{1,2,...,n-1}.

 
 

A BC oldalt a-val jelölve: CNx=an⋅x és BNx=an(n-x).
Mindkét háromszög területét T és három kisebb háromszög területösszegének különbségeként írhatjuk fel:
TNxFH1▵=T-(TAFH1▵+TBFNx▵+TCH1Nx▵),(1)TNxFH2▵=T-(TAFH2▵+TBFNx▵+TCH2Nx▵).(2)

Írjuk fel a kis háromszögek területét (felhasználjuk, hogy ha két háromszögben a megfelelő két oldal által bezárt szög megegyezik, akkor a területek aránya az oldalak arányának a szorzatával egyenlő):
TAFH1▵=12⋅23⋅T=T3,TAFH2▵=12⋅13⋅T=T6,TBFNx▵=12⋅n-xn⋅T=T(n-x)2n,TCH1Nx▵=13⋅xn⋅T=Tx3n,TCH2Nx▵=23⋅xn⋅T=2Tx3n.

Ezeket (1)-be és (2)-be beírva kapjuk, hogy:
TNxFH1▵=T(1-13-n-x2n-x3n)=T⋅n+x6n,(1')TNxFH2▵=T(1-16-n-x2n-2x3n)=T⋅2n-x6n.(2')
Különböző x értékekre TNxFH1▵ értéke is más lesz, és ugyanez igaz TNxFH2▵ értékére is. Tehát az egyenlő területű háromszög-párokat csak így kereshetjük:
TNxFH1▵=TNyFH2▵,vagyisT⋅n+x6n=T⋅2n-y6n,ahonnanx+y=n.


Látható, hogy minden x értékhez pontosan egy y érték tartozik. Ezzel az állítást beláttuk.
 
II. megoldás. A harmadik oldal két végpontját jelölje N0 és Nn. Feltehetjük, hogy a jelölések úgy vannak megválasztva, hogy az N0,N1,...,Nn pontok ebben a sorrendben követik egymást, továbbá H1 éppen az N0H2 szakasz felezőpontja. Ekkor az NiNi+1 szakaszok (0≤i<n) mind egyenlő hosszúak, legyen ez a hossz y.
Ha a háromszög területe T, akkor az N0H1F és az NnH2F háromszögek területe egyaránt T6, az N0H2F és NnH1F háromszögeké pedig T3, hiszen ha két háromszögben a megfelelő két oldal által bezárt szög megegyezik, akkor a területek aránya az oldalak arányának a szorzatával egyenlő.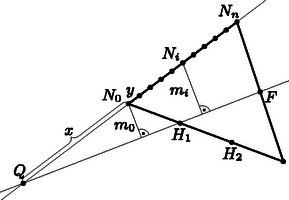
 
 

Jelölje mi az NiH1F háromszög H1F oldalhoz tartozó magasságát, Q az N0Nn és a H1F egyenes metszéspontját, és legyen x=QN0. A párhuzamos szelők tétele szerint mim0=x+iyx, amiből
mi=m0(1+iyx)=m0+(m0⋅yx)⋅i.
Ebből pedig már következik, hogy az NiH1F háromszögek H1F oldalhoz tartozó magassága egy n+1 hosszúságú növekvő számtani sorozatot alkot, melynek első tagja m0, differenciája pedig m0⋅yx. Ennek megfelelően az NiH1F háromszögek területe egy olyan n+1 tagú növekvő számtani sorozatot alkot, melynek első eleme T6, az utolsó pedig T3. Legyen ez a sorozat an. Hasonlóképpen az NiH2F háromszögek területe egy olyan n+1 tagú csökkenő számtani sorozat, amelynek első eleme T3, az utolsó pedig T6. Legyen ez a sorozat bn. A két számtani sorozat egyaránt (n+1) tagból áll, a1=bn+1, b1=an+1. Ezen két észrevételből adódik, hogy ai=bn+2-i, amiből már következik a feladat állítása.