Kezdőlap


Feladat:	B.4017	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Csizmadija Laura , Fonyó Dávid , Réti Dávid , Szalai Szilárd
Füzet:	2008/szeptember, 333 - 335. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai bizonyítások, Körérintők, Középponti és kerületi szögek, Eltolás, Feladat
Hivatkozás(ok):	Feladatok: 2007/szeptember: B.4017

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen $e$ a két kör közös érintője, 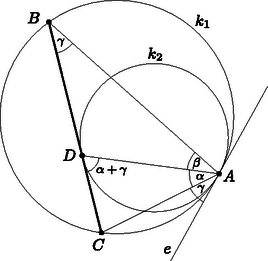$C A D ∢ = α$ , $B A D ∢ = β$ , $A B C ∢ = γ$ .

1. ábra

A kerületi szögek tételét felhasználva a

C A

ívhez tartozó

γ

kerületi szög megegyezik a

C A

húr és az

e

érintő által közbezárt érintő szárú kerületi szöggel. A

C D A ∢

k_{2}

körben a

D A

ívhez tartozó érintő szárú kerületi szög, ezért megegyezik a

D A

húr és az e érintő által bezárt

α + γ

nagyságú érintő szárú kerületi szöggel. Tehát az

A B D

háromszög

D

csúcsánál lévő külső szöge

α + γ

, ez megegyezik a háromszög másik két csúcsánál lévő belső szögek összegével:

α + γ = β + γ

. Így

α = β

, ezt kellett bizonyítanunk.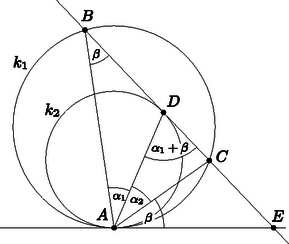

II. megoldás. Vizsgáljuk először azt az esetet, amikor a

k_{2}

kör

A

és

D

pontbeli érintője egy

E

pontban metszi egymást (2. ábra). Vezessük be az alábbi jelöléseket:

\begin{matrix} B A D ∢ = α_{1}, D A C ∢ = α_{2}, C B A ∢ = β . \end{matrix}

Ekkor

C B A ∢ = C A E ∢ = β

, mivel a

k_{1}

körben, azonos

A C

húrhoz tartozó kerületi és érintőszárú kerületi szögek. Ezt felhasználva:

\begin{matrix} D A E ∢ = D A C ∢ + C A E ∢ = α_{2} + β . \end{matrix}

A D B

háromszögre alkalmazva a külsőszög-tételt:

\begin{matrix} E D A ∢ = B A D ∢ + D B A ∢ = α_{1} + β . \end{matrix}

Mivel az

E

pontból a

k_{2}

körhöz húzott érintőszakaszok egyenlő hosszúságúak, a

D A E

háromszög egyenlő szárú, és

E D A ∢ = D A E ∢

, vagyis

α_{1} + β = α_{2} + β

, amiből

α_{1} = α_{2}

2. ábra

Abban az esetben, ha a

k_{2}

kör

A

és

D

pontbeli érintője párhuzamos egymással, akkor az

A D

szakasz a

k_{2}

kör egy átmérője, melynek egyenesére illeszkedik a két kör középpontja is (3. ábra). Az

A D

egyenes szimmetriatengelye a két körnek, és így az

A B C

egyenlő szárú háromszögnek is, vagyis az

α_{1} = α_{2}

egyenlőség most is teljesül.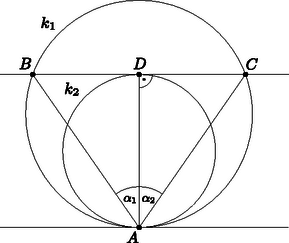

3. ábra

III. megoldás. Ha a

k_{2}

kör belülről érinti a

k_{1}

kört, akkor a közös érintési pont,

A

egy

H

középpontos hasonlósági transzformáció középpontja, mely a

k_{2}

kört a

k_{1}

körre képezi le.
Az

A B

szakasz a

k_{2}

kört

B_{2}

-ben, az

A C

szakasz

C_{2}

-ben metszi.
A

H

traszformáció a

B_{2}

pontot

B

-be, a

C_{2}

pontot

C

-be, a

D

pontot pedig

D_{1}

-be viszi át, a

k_{2}

kör

e_{2}

érintőjének képe pedig a

k_{1}

kör

e_{1}

érin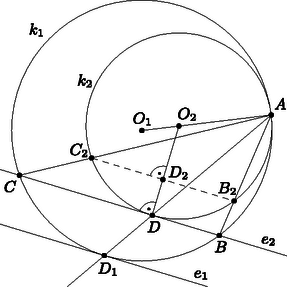tője.

4. ábra

Emiatt a

B_{2} C_{2}

szakasz, az

e_{1}

és

e_{2}

érintők egymással párhuzamosak.
Az

e_{2}

érintő a

D

érintési pontban merőleges az

O_{2} D

sugárra, így a

B_{2} C_{2}

szakasz is merőleges az

O_{2} D

sugárra.
A

B_{2} C_{2}

szakasz a

k_{2}

körben húr,

O_{2} D

pedig a húr felező merőlegese, így a

B_{2} D

ív és a

C_{2} D

ív egyenlőek. Ezeket az íveket a

H

traszformáció a

k_{1}

kör

B D_{1}

és

C D_{1}

íveibe képezi, tehát ezek is egyenlőek, vagyis az ezekhez tartozó

A

csúcsú kerületi szögek is egyenlőek a

k_{1}

körben, tehát

C A D_{1} ∢ = D_{1} A B ∢

, vagyis

C A D ∢ = D A B ∢

, és ezt kellett bizonyítani.