Kezdőlap


Feladat:	C.913	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Besnyõ Réka , Pálovics Péter
Füzet:	2008/szeptember, 331 - 332. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai bizonyítások, Beírt kör, Hozzáírt körök, Deltoidok, Téglalapok, C gyakorlat
Hivatkozás(ok):	Feladatok: 2007/október: C.913

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. A háromszög szögeit a szokásos módon jelöljük.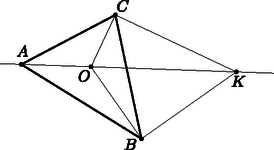

I. megoldás. Először azt vizsgáljuk meg, hogy a

B K C O

négyszög mikor lesz deltoid.

Ha egy négyszög deltoid, akkor két szemben fekvő szöge és két-két szomszédos oldala megegyezik. Ez utóbbira két lehetőség van.
Az első:

O B = O C

és

K B = K C

. Ekkor a

C O B

háromszög egyenlő szárú, így alapon fekvő szögei egyenlők:

B C O ∢ = C B O ∢

. Mivel

O B

és

O C

szögfelezők, így ebből

A C B ∢ = A B C ∢

következik, tehát az

A B C

háromszögben

γ = β

, a háromszög egyenlő szárú.
Ha az

A B C

háromszög egyenlő szárú, akkor az

A

csúcshoz tartozó szögfelező egyben a

B C

oldal felező merőlegese is, és mivel

O

és

K

is ezen a felező merőlegesen van,

O B = O C

és

K B = K C

, a négyszög deltoid.
A másik lehetőség:

O C = K C

O B = K B

és

C O B ∢ = C K B ∢

. Mivel egy szög külső és belső szögfelezői merőlegesek egymásra,

O C K ∢ = O B K ∢ = 90^{\circ}

, és így:

\begin{matrix} C O B ∢ = C K B ∢ = \frac{360^{\circ} - (90^{\circ} + 90^{\circ})}{2} = 90^{\circ} . \end{matrix}

C O B

háromszögben

O B C ∢ = β / 2 = 180^{\circ} - (90^{\circ} + γ / 2)

, amiből

β + γ = 180^{\circ}

következik, ez azonban háromszög esetén lehetetlen.
Ha a

B K C O

négyszög téglalap, akkor összes szöge, így a

C O B ∢

is derékszög, ami a fentiek miatt nem lehetséges.
Összefoglalva: a négyszög pontosan akkor deltoid, ha

A B = A C

, és sohasem téglalap.

Másik bizonyítás arra, hogy deltoid esetén a háromszög szükségképpen egyenlő szárú.
Ha a

B K C O

négyszög deltoid, akkor átlói merőlegesek egymásra, vagyis

C B ⊥ O K

. Mivel

O K

α

szögfelezőjére illeszkedik ez azt jelenti, hogy

B C

merőleges az

α

szögfelezőjére, így a háromszög egyenlő szárú.

II. megoldás arra, hogy a négyszög sosem lesz téglalap.
Ismert, hogy a hozzáírt kör sugara nagyobb a beírt kör sugaránál. Ez következik például Kiss György: Amit jó tudni a háromszögekről c. cikkének¹ a 8. állításából, mely szerint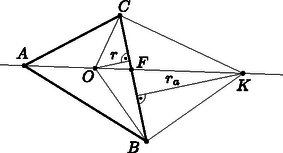

\begin{matrix} T = r \cdot s = r_{a} (s - a) = r_{b} (s - b) = r_{c} (s - c) \end{matrix}

(ahol például

r_{a}

a

oldalhoz írt kör sugarát,

r

pedig a beírt kör sugarát jelöli).

Ha a

B K C O

négyszög téglalap, akkor az átlói által meghatározott négy háromszög egybevágó, tehát ekkor

O F C ▵ ≅ K F B ▵

. Ha két háromszög egybevágó, akkor megfelelő szakaszaik egyenlő hosszúak, így például az

F C

és az

F B

oldalhoz tartozó magasságok megegyeznek. Ez a két magasság a beírt és a hozzáírt kör sugara:

r = r_{a}

, ami ellentmond a fenti állításnak. A négyszög tehát nem lehet téglalap.

¹http://www.komal.hu/cikkek/kissgy/haromszogekrol/amitjotudni.h.shtml