Feladat: B.3939 Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Aujeszky Tamás ,  Keresztfalvi Tibor ,  Szirmay-Kalos Barnabás 
Füzet: 2007/április, 227 - 228. oldal  PDF  |  MathML 
Témakör(ök): Síkgeometriai számítások trigonometria nélkül, Háromszög területe, Pitagorasz-tétel alkalmazásai, Szögfüggvények, síkgeometriai számítások, Pont körüli forgatás, Feladat
Hivatkozás(ok):Feladatok: 2006/október: B.3939

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jelölje az ABC háromszög derékszögű csúcsát C. Ekkor a CA és CB oldalegyeneseket meghosszabbítva a háromszöget belehelyezhetjük egy egységnyi oldalhosszú CGPF négyzetbe. Mivel a CP átló hossza 2, így P éppen a keresett pont, vagyis a BPA szöget kell meghatároznunk. (Megjegyzés: igazolható, hogy az ABC háromszög befogói 1 egységnél rövidebbek.)

 
 

Az ABC háromszög oldalait jelölje a szokásos módon a, b és c, továbbá a P pontból AB-re állított merőleges talppontját jelöljük E-vel, végül legyen PE=x (lásd az ábrát). A négyzet területe egységnyi, így
xc2+ab2+1-a2+1-b2=1.
Mivel a háromszög kerülete 2, azért
c=2-a-b.
Ezt az előző egyenletbe behelyettesítve kapjuk, hogy
x=a+b-ab2-a-b.

A Pitagorasz-tétel alapján a2+b2=c2=(2-a-b)2, a négyzetre emelés és az egyszerűsítés után ez az egyenlet 4-4a-4b+2ab=0 alakra hozható, amiből pedig 2-a-b=a+b-ab. Ezt a korábbi, x-re kapott összefüggésbe behelyettesítve x=1-et kapunk.
Mivel GP=EP=1, azért a PGB és PEB derékszögű háromszögek egybevágók. Hasonlóan belátható a PEA és PFA háromszögek egybevágósága is. Ebből következik, hogy GPB∢=BPE∢, illetve EPA∢=APF∢. Vagyis a BPA szög a GPF derékszög fele, azaz BPA∢=BPE∢+EPA∢=45∘-os szögben látszik az átfogó a kérdéses pontból.
 
Megjegyzés. A PG=PE=PF egyenlőségből kapjuk, hogy a P pont éppen a háromszög átfogójához hozzáírt kör középpontja. Ismeretes, hogy derékszögű háromszögben az átfogóhoz írt kör sugara egyenlő a félkerülettel ‐ ami jelen esetben 1 egység ‐, az állítás lényegében a fenti megoldásban alkalmazott gondolatmenettel bizonyítható. Továbbá a külső pontból körhöz húzott érintőszakaszok hossza egyenlő, így PGBE és PEAF deltoidok, amiből szintén megkaphatjuk a feladat megoldását.
 
II. megoldás. Használjuk az előző megoldás ábráját, legyen továbbá APF∢=α és GPB∢=β. Az előző megoldásban igazolt 4-4a-4b+2ab=0 egyenletet átrendezve
a=2-2b2-b=2-22-b.
Ekkor AF=1-b és BG=1-a=22-b-1. Továbbá
tgα=1-b1,valaminttgβ=22-b-11.
A tangensfüggvény addíciós képletét felhasználva
tg(α+β)=tgα+tgβ1-tgαtgβ=(1-b)+(22-b-1)1-(1-b)(22-b-1)=(1-b)(2-b)+b(2-b)-(1-b)b=1.
Tehát tg(α+β)=1, amiből α+β=45∘. Mivel BPA∢=90∘-(α+β)=45∘, azért a keresett szög nagysága 45∘.
 

Megjegyzés. Szögfüggvények használatával egy másik megoldást is kaphatunk, ha először felírjuk a PBC és CAP háromszögek PB, illetve PA oldalára a koszinusztételt (innen PB2=a2-2a+2 és PA2=b2-2b+2 adódik), majd újból alkalmazzuk a koszinusztételt a PBA háromszög BA oldalára (amiből cosAPB∢=12 adja a végeredményt). Néhányan ugyanezt a megoldást koordináta-geometriai úton igazolták, ekkor az APB szög nagysága a PA→ és PB→ vektorok skaláris szorzatából számítható ki.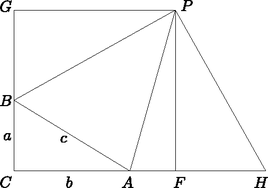
 
III. megoldás. Használjuk az előző megoldások jelöléseit. Forgassuk el a PGB háromszöget P körül pozitív irányban 90∘-kal. Mivel PG=PF, GPF∢=90∘ és PGB∢+PFA∢=180∘, azért a forgatás után a PFH háromszöget kapjuk, amelynek H csúcsa rajta van az AF egyenesen.
 
 

Mivel PA=PA, PB=PH (a forgatás miatt), valamint AH=AF+FH=(1-b)+(1-a)=2-a-b=c=AB, azért az APB és APH háromszögek egybevágók, ebből adódóan BPA∢=APH∢. A forgatás alapján BPH∢=90∘, innen tehát BPA∢=90∘2=45∘.