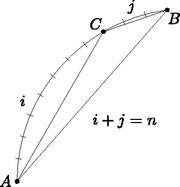|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Megoldás. A 2003 egymást nem metsző átló a sokszöget 2004 háromszögre bontja, amelyek csúcsai a csúcsai. Nevezzünk egy ilyen háromszöget jónak, ha két oldala jó és egyenlő szárú.
Legyen a sokszög egy átlója vagy oldala, és jelöljük -nel az csúcsokat összekötő, sokszögoldalakból álló két töröttvonal közül a rövidebbik (nem hosszabbik) oldalainak a számát (). A megrajzolt átlók azt a sokszöget is háromszögekre bontják, amelyet az oldalszakaszból álló töröttvonal és az szakasz határol. (Ha , azaz a egy oldala, akkor a sokszög szakasszá fajul, a háromszögek száma 0.) Jelöljük -nel, hogy ezt a sokszöget az -t és egymást nem metsző átlók megrajzolásával (az eredeti felbontás átlói közül ilyen van) háromszögekre bontva legfeljebb hány jó háromszög jöhet létre. Az -re vonatkozó teljes indukcióval bebizonyítjuk, hogy .
Ha , akkor és szomszédos csúcsok -ben, egyetlen háromszög sem jön létre -ben, így jó sem, . Ha , akkor és másodszomszédos csúcsok -ben, a létrejövő egyetlen háromszög jó, , az állítás igaz. Legyen most és tegyük föl, hogy , ha . Tekintsük a sokszögnek azt a felbontását, amelynek során jó háromszöget kapunk. Ebben a felbontásban a létrejövő háromszögek egyikének oldala az , legyen e háromszög harmadik csúcsa (2. ábra). Ha az oldalt , a -t pedig hosszúságú töröttvonal köti össze, akkor és . Ekkor nyilván | |
Az első esetben az indukciós föltevést tagonként alkalmazva és felhasználva, hogy ⌊x⌋+⌊y⌋≤⌊x+y⌋: | f(n)=f(i)+f(j)≤⌊i2⌋+⌊j2⌋≤⌊i+j2⌋=⌊n2⌋. |
Nézzük meg, hogyan lehetséges a második eset. A P1 megválasztása miatt AB a leghosszabb a P1 csúcsait összekötő szakaszok közül, így az ABC háromszögben is AB a leghosszabb oldal. Ez a háromszög tehát csak úgy lehet egyenlő szárú, ha AC=CB. Egy egyenlő szárú háromszögnek vagy mindkét szára jó, vagy egyik sem az (a háromszögnek és P-nek közös szimmetriatengelye van), így ha az egyenlő szárú ABC háromszög jó, akkor az AC és BC szárak a jó oldalai. Ekkor i és j egyenlő páratlan számok, azaz n=4k+2 alakú. Az indukciós feltevés szerint f(n2)≤[n2] és így | f(n)=f(n2)+f(n2)+1≤2⌊n4⌋+1=2⋅k+1=⌊n2⌋, |
az indukciós lépést igazoltuk.
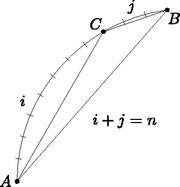 2. ábra
Tekintsük ezek után a P sokszög megrajzolt átlóit. Ha van köztük olyan, amelyik áthalad a sokszög középpontján, akkor a jó háromszögek maximális száma | f(1003)+f(1003)≤2⋅⌊10032⌋=1002. |
Ha ilyen átló nincsen, akkor tekintsük a felbontásban szereplő háromszögek közül azt, amelyik a belsejében tartalmazza a sokszög középpontját. Ennek bármely két csúcsát a P félkerületénél rövidebb töröttvonal köti össze, álljanak ezek rendre a,b,c szakaszból. (a+b+c=2006.) Ha ez a háromszög jó, akkor a, b és c közül kettő páratlan, a felbontás összesen legfeljebb | 1+⌊a2⌋+⌊b2⌋+⌊c2⌋=1+a+b+c2-1=1003, |
ha pedig nem jó, akkor legfeljebb | ⌊a2⌋+⌊b2⌋+⌊c2⌋≤⌊a+b+c2⌋=1003 |
jó háromszöget tartalmaz.
A kapott felső korlát éles, 1003 jó háromszög jön létre, ha a másodszomszédos csúcsokat kötjük össze, a ,,belső'' 1003 oldalú sokszöget pedig további 1000 átló megrajzolásával tetszőleges módon háromszögekre bontjuk. |
 PDF |
PDF |  MathML
MathML