Kezdőlap


Feladat:	B.4014	Korcsoport: 16-17	Nehézségi fok: könnyű
Megoldó(k):	Anda Roland , Balási Szabolcs , Horovitz Gábor
Füzet:	2008/május, 286 - 288. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai bizonyítások, Háromszög területe, Középpontos tükrözés, Vektorok vektoriális szorzata, Feladat
Hivatkozás(ok):	Feladatok: 2007/szeptember: B.4014

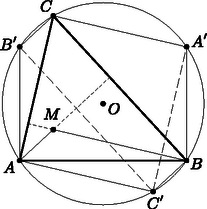
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A középpontos tükrözés tulajdonságaiból adódóan az $A C' A' C$ , $A B A' B'$ és a $B C B' C'$ négyszögek téglalapok, hiszen átlóik egyenlő hosszúak és felezik egymást.
Jelölje $M$ a háromszög magasságpontját. Ekkor $B M$ párhuzamos $A C'$ -vel, mivel mindkettő derékszöget zár be $A C$ -vel. Hasonlóan $A M$ párhuzamos $C' B$ -vel. Így az $A M B C'$ négyszög paralelogramma. Ennek átlója $A B$ , ami felezi a területét, így $A M B$ területe egyenlő $A B C'$ területével. Hasonlóan belátható, hogy $A C B'$ területe egyenlő $A C M$ területével, és $B C A'$ területe egyenlő $B C M$ területével. Tehát az $A' B C$ , $A B' C$ , $A B C'$ háromszögek területének összege egyenlő a $B C M$ , az $A C M$ és az $A M B$ háromszögek területének összegével, ami éppen az eredeti $A B C$ háromszög területe.

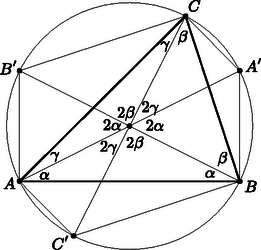
II. megoldás. Az

A O C

B O C

és

A O B

egyenlő szárú háromszögekben (a kerületi és középponti szögek tétele szerint, az ábrán láthatóan):

\begin{matrix} 2 α + 2 β & = & 180^{\circ} - 2 γ, \\ 2 α + 2 γ & = & 180^{\circ} - 2 β, \\ 2 γ + 2 β & = & 180^{\circ} - 2 α . \end{matrix}

Írjuk föl az

A B C

háromszög területét

T_{A B C ▵} = T_{A O C ▵} + T_{C O B ▵} + T_{B O A ▵}

alakban. Itt (a

T_{▵} = \frac{x y sin δ}{2}

képletet felhasználva):

\begin{matrix} T_{A B C ▵} & = & \frac{r^{2} sin (180^{\circ} - 2 γ)}{2} + \frac{r^{2} sin (180^{\circ} - 2 β)}{2} + \frac{r^{2} sin (180^{\circ} - 2 α)}{2} = \\ = & \frac{r^{2} sin 2 γ}{2} + \frac{r^{2} sin 2 β}{2} + \frac{r^{2} sin 2 α}{2} . \end{matrix}

Hasonlóan az

A B' C A' B C'

hatszög területe:

\begin{matrix} T_{A B' C A' B C'} & = & T_{A O B'} + T_{B' O C} + T_{C O A'} + T_{A' O B} + T_{B O C'} + T_{C' O A} = \\ = & 2 \frac{r^{2} sin 2 α}{2} + 2 \frac{r^{2} sin 2 β}{2} + 2 \frac{r^{2} sin 2 γ}{2}, \end{matrix}

ami éppen a kétszerese a

T_{A B C ▵}

-nek. Ez éppen azt jelenti, hogy az

A' B C

A B' C

és

A B C'

háromszögek területének összege egyenlő az

A B C

háromszög területével.

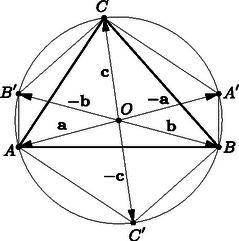
III. megoldás. Jelölje a háromszög körülírt körének középpontjából az

A

B

C

pontokba mutató vektorokat

a

b

és

c

. A tükrözés miatt az

A'

B'

C'

pontok helyvektorai ekkor

- a

- b

és

- c

Egy háromszög területe fele akkora, mint két, egy csúcsból induló oldalvektora vektoriális szorzatának a hossza. Írjuk föl ezzel a szóban forgó háromszögek területét; mivel valamennyi helyvektor a síkban van, vektoriális szorzatuk a síkra merőleges, és a szorzás megfelelő sorrendje esetén egymással azonos állású. Így megtehetjük, hogy hosszuk helyett magukkal a (vektoriális szorzatként kapott) vektorokkal számolunk:

\begin{matrix} T_{A B C ▵} & = \frac{1}{2} \cdot \vec{C B} \times \vec{C A} = \frac{1}{2} \cdot (b - c) \times (a - c), & (1) \\ T_{A B C' ▵} & = \frac{1}{2} \cdot \vec{C' A} \times \vec{C' B} = \frac{1}{2} \cdot (a + c) \times (b + c), \\ T_{A B' C ▵} & = \frac{1}{2} \cdot \vec{B' C} \times \vec{B' A} = \frac{1}{2} \cdot (c + b) \times (a + b), \\ T_{A' B C ▵} & = \frac{1}{2} \cdot \vec{A' B} \times \vec{A' C} = \frac{1}{2} \cdot (b + a) \times (c + a) . \end{matrix}

A három külső háromszög területének összege:

\begin{matrix} \sum T' = \frac{1}{2} \cdot ((a + c) \times (b + c) + (c + b) \times (a + b) + (b + a) \times (c + a)) . \end{matrix}

Felbontva a zárójeleket, és kihasználva, hogy

x \times y = - y \times x

, valamint

x \times x = 0

, azt kapjuk, hogy

\begin{matrix} \sum T' = \frac{1}{2} \cdot (c \times b + b \times a + a \times c) . \end{matrix}

Felbontva (1)-ben a zárójeleket

\begin{matrix} T_{A B C ▵} = \frac{1}{2} \cdot (b \times a - c \times a - b \times c) = \frac{1}{2} \cdot (c \times b + b \times a + a \times c) . \end{matrix}

A két terület valóban megegyezik.