Kezdőlap


Feladat:	4007. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Kupcsik Réka , Rárósi Dávid
Füzet:	2008/április, 237 - 238. oldal		PDF \| MathML
Témakör(ök):	Kinetikus gázelmélet, Tökéletesen rugalmas ütközések, Feladat
Hivatkozás(ok):	Feladatok: 2007/október: 4007. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jelöljük az ütközés előtti sebességvektorokat $v_{1}$ -gyel és $v_{2}$ -vel, az ütközés utáni sebességvektorokat pedig $v_{1}'$ -vel és $v_{2}'$ -vel, a héliumatomok tömegét pedig $m$ -mel! A feladat szövege szerint $| v_{1} | = v_{1} = 800$ m/s és $| v_{2} | = v_{2} = 600$ m/s.
A rugalmas ütközés során megmarad az ütköző molekulák összimpulzusa és összenergiája:

\begin{matrix} m v_{1} + m v_{2} = m v_{1}' + m v_{2}', \\ \frac{1}{2} m v_{1}^{2} + \frac{1}{2} m v_{2}^{2} = \frac{1}{2} m v_{1}'^{2} + \frac{1}{2} m v_{2}'^{2}, \end{matrix}

azaz

\begin{matrix} v_{1} + v_{2} = v_{1}' + v_{2}', & (1) \\ v_{1}^{2} + v_{2}^{2} = v_{1}'^{2} + v_{2}'^{2} . & (2) \end{matrix}

Az impulzusmegmaradást kifejező egyenletet az ábrán látható vektorösszeggel is szemléltethetjük. Tudjuk, hogy az ütközés előtti sebességek azonos irányúak, emiatt fennáll:

\begin{matrix} {| v_{1} + v_{2} |}^{2} = {(v_{1} + v_{2})}^{2} . \end{matrix}

Írjuk most fel az

A B C

háromszögre a koszinusz-tételt:

\begin{matrix} v_{1}'^{2} + v_{2}'^{2} - 2 v_{1}' v_{2}' cos (180^{\circ} - α) = {(v_{1} + v_{2})}^{2}, \end{matrix}

(3)

ahonnan az ütközés utáni sebességvektorok keresett

α

szögének koszinusza kifejezhető:

\begin{matrix} cos α = \frac{[v_{1}^{2} + v_{2}^{2} - v_{1}'^{2} - v_{2}'^{2}] + 2 v_{1} v_{2}}{2 v_{1}' v_{2}'} . \end{matrix}

(4)

A szögletes zárójelben álló kifejezés (2) miatt nulla, így (4) a következő egyszerű alakba írható:

\begin{matrix} cos α = \frac{v_{1} v_{2}}{v_{1}' v_{2}'} . \end{matrix}

(5)

Alkalmazzuk a mértani- és a négyzetes közepekre vonatkozó

\begin{matrix} v_{1}' v_{2}' \leq \frac{v_{1}'^{2} + v_{2}'^{2}}{2} \end{matrix}

egyenlőtlenséget, amely

{(v_{1}' - v_{2}')}^{2} \geq 0

nyilvánvaló következménye! Ennek segítségével és (2) kihasználásával (5) így alakul:

\begin{matrix} cos α \geq \frac{2 v_{1} v_{2}}{v_{1}'^{2} + v_{2}'^{2}} = \frac{2 v_{1} v_{2}}{v_{1}^{2} + v_{2}^{2}} = \frac{2 \cdot 800 \cdot 600}{800^{2} + 600^{2}} = 0, 96, \end{matrix}

ahonnan

α \leq 16, 26^{\circ}

. A héliumatomok ütközés utáni sebessége tehát legfeljebb ekkora szöget zárhat be egymással, és az egyenlőség akkor áll fenn, amikor

v_{1}' = v_{2}'

II. megoldás. Vizsgáljuk a folyamatot a

\frac{v_{1} + v_{2}}{2} = 700 \frac{m}{s}

sebességgel mozgó tömegközépponti rendszerből! Innen nézve a két atom ugyanakkora,

100 \frac{m}{s}

nagyságú, de ellentétes irányú sebességgel közeledik egymáshoz. Az ütközés után is egymással ellentétes irányban, változatlan nagyságú sebességgel kell mozogjanak, csak így teljesülhet az energiamegmaradás és az impulzusmegmaradás törvénye.
Az eredeti koordináta-rendszerbe úgy térhetünk vissza, ha a tömegközépponti rendszerbeli sebességekhez hozzáadjuk a tömegközéppont

700 \frac{m}{s}

nagyságú sebességét (lásd az ábrát, melyet az áttekinthetőség kedvéért 100-szorosan lecsökkentett sebességnagyságokkal rajzoltunk fel).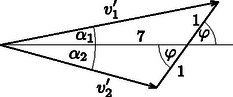

A feladat hátralévő részében azt vizsgáljuk, hogy

φ

függvényében milyen értékeket vehet fel az

α = α_{1} + α_{2}

szög. Számítsuk ki

tg α

-t az addíciós tétel felhasználásával:

\begin{matrix} tg α = tg (α_{1} + α_{2}) = \frac{tg α_{1} + tg α_{2}}{1 - tg α_{1} tg α_{2}} = \frac{\frac{sin φ}{7 + cos φ} + \frac{sin φ}{7 - cos φ}}{1 - \frac{sin φ}{7 + cos φ} \frac{sin φ}{7 - cos φ}} = \frac{7}{24} sin φ . \end{matrix}

Látható, hogy a

0 \leq φ \leq 180^{\circ}

értelmezési tartományban

0 \leq tg α \leq \frac{7}{24}

, vagyis

0 \leq α \leq 16, 26^{\circ}

. Az ütközés utáni sebességvektorok szöge akkor maximális, amikor

φ = 90^{\circ}

, ilyenkor

v_{1}' = v_{2}'