Feladat: B.4030 Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Dinh Hoangthanh Attila ,  Horváth Vanda ,  Márkus Bence ,  Somogyi Ákos ,  Szõke Nóra ,  Tubak Dániel 
Füzet: 2008/április, 222 - 224. oldal  PDF  |  MathML 
Témakör(ök): Mértani helyek, Szögfelező egyenes, Háromszögek geometriája, Feladat
Hivatkozás(ok):Feladatok: 2007/október: B.4030

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Annak megfelelően, hogy a C pont A-hoz vagy B-hez van közelebb, két lényegileg különböző esetet kell figyelembe vennünk. Alábbi megoldásunk egyszerre működik mindkét esetben (lásd az ábrákat).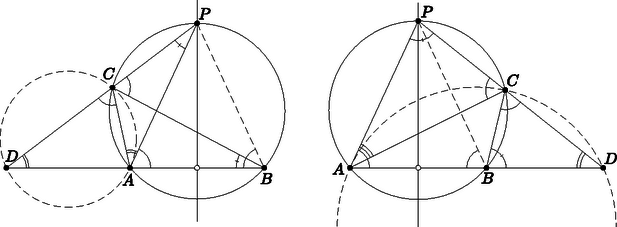

 
 

Az, hogy a DP egyenes külső szögfelező a C csúcsban, egyenérékű azzal, hogy a C-nél jelölt szögek egyenlők. Mivel az AP egyenes érinti az ADC kört, a kerületi szögek tétele miatt ADC∢=PAC∢. Ezen szögek egyenlőségéből adódik, hogy a DCB és az ACP háromszög hasonló. Így a B és a P csúcsoknál levő szögeik is egyenlők. Ez viszont azt jelenti, hogy az ABCP négyszög húrnégyszög. Ebből következik, hogy az ABP háromszög A-nál és B-nél levő szöge is egyenlők egymással. Tehát az APB háromszög egyenlőszárú, vagyis P nem más, mint az ABC körív és az AB szakasz felezőmerőlegesének a metszéspontja.
A megfordításhoz tekintsük az AB szakasz felező merőlegesének egy tetszőleges olyan Q pontját, amely nem esik az AB szakaszra. Azt kell megmutatnunk, hogy ez a pont hozzátartozik a P pontok mértani helyéhez. Ám ha az ABQ háromszög köré írható kör rövidebbik QA ívén felveszünk egy C pontot úgy, hogy sem CA, sem CB ne legyen egyenlő AB-vel, akkor az elmondottak alapján világos, hogy az ehhez tartozó P pont nem lehet más, mint Q. Tehát a mértani hely az AB szakasz felezőmerőlegese a felezőpontja kivételével.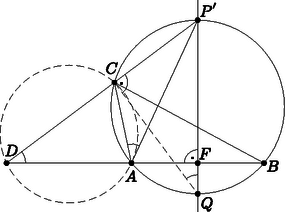
 
II. megoldás. Az AB szakasz felezőmerőlegese messe az ABC kör ACB ívét P'-ben, a másik ívét Q-ban. Az AB szakasz felezőpontját jelölje F. Bebizonyítjuk, hogy a C-beli külső szögfelező és az A-beli érintő is átmegy P'-n, vagyis P'=P.
 
 

ACQ∢=QCB∢, mivel egyenlő íveken nyugvó kerületi szögek, így CQ az ACB∢ belső szögfelezője. A C-beli külső szögfelező merőleges a belsőre, amire CP' is merőleges a Thalesz-tétel miatt. Így ezek egy egyenesbe esnek, tehát a külső szögfelező átmegy P'-n.
Tekintsük a P'FD és P'CQ háromszögeket. A P'-nél levő szögük megegyezik, és van még egy-egy derékszögük. Tehát a D és Q csúcsuknál levő szögeik is egyenlők. Utóbbi továbbá egyenlő az A pontnál megjelölt szöggel, mivel azonos ívhez tartozó kerületi szögek.
Azt kaptuk, hogy a D-nél és A-nál a jelölt szögek egyenlők. Az előbbi az ACD háromszög körülírt körében az AC-hez tartozó kerületi szög. Tudjuk, hogy ezzel egyenlő az A-ban a körhöz húzott érintő AC egyenessel bezárt szöge, tehát ez az érintő csak AP' lehet.
(A P'BC∢ is egyenlő a Q-nál levő szöggel, tehát a BCD körhöz B-ben húzott érintő is átmegy P'-n. Vagyis, ha felcseréljük A-t és B-t, akkor is igaz lesz, hogy P=P'. Tehát ha C közelebb van A-hoz, mint B-hez, akkor is működik a bizonyítás.)
Tehát minden C pont esetén az a pont lesz P, amit az ACB körív kimetsz AB felezőmerőlegeséből. Amíg C befutja a sík pontjait (legalábbis amire ABC nem egyenlőszárú háromszög), a kimetszett P pontok a felezőmerőleges összes pontját kiadják, AB felezőpontját leszámítva. Tehát a mértani hely az AB szakasz felezőmerőlegese a felezőpontja kivételével.