Kezdőlap


Feladat:	B.4027	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Fonyó Dávid , Lovas Lia Izabella
Füzet:	2008/április, 220 - 221. oldal		PDF \| MathML
Témakör(ök):	Irracionális egyenletek, Inverz függvények, Harmadfokú (és arra visszavezethető) egyenletek, Feladat
Hivatkozás(ok):	Feladatok: 2007/október: B.4027

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. Az egyenletben szereplő tört és négyzetgyökös kifejezés értelmezhetősége miatt $x \neq 6$ és $\frac{11 x - 6}{6 - x} \geq 0$ , amely feltételek $x \in [\frac{6}{11}; 6 [$ esetén teljesülnek.
Az egyenletet 6-tal beszorozva:

\begin{matrix} \frac{6 (x^{2} + 1)}{x^{2} + 11} = \sqrt[]{\frac{11 x - 6}{6 - x}} . \end{matrix}

\begin{matrix} f (x) = \frac{6 (x^{2} + 1)}{x^{2} + 11} = 6 (1 - \frac{10}{x^{2} + 11}) \end{matrix}

függvény az értelmezési tartományán szigorúan monoton növekvő, így ott invertálható, és az inverze

\begin{matrix} f^{- 1} (x) = \sqrt[]{\frac{11 x - 6}{6 - x}} . \end{matrix}

Tehát az egyenlet jobb oldalán álló kifejezés a bal oldal inverze.
Mivel egy függvény és inverzének képe az

y = x

egyenesre tükrös, egyenlőségük csak

y = x

esetben teljesülhet. Eredeti egyenletünk tehát ekvivalens a

\begin{matrix} \frac{6 (x^{2} + 1)}{x^{2} + 11} = x \end{matrix}

egyenlettel. Rendezve:

0 = x^{3} - 6 x^{2} + 11 x - 6

. Szorzattá alakítva:

\begin{matrix} 0 = (x - 1) (x - 2) (x - 3) . \end{matrix}

Ennek alapján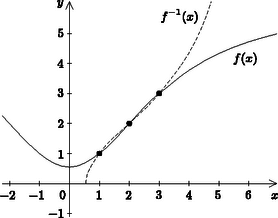

x_{1} = 1

x_{2} = 2

x_{3} = 3

A kapott gyökök kielégítik az egyenletet, hiszen valamennyien az

f

értelmezési tartományához tartoznak.