Kezdőlap


Feladat:	B.3959	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Godó Zita , Gresits Iván , Németh Kitti Noémi , Sümegi Károly
Füzet:	2008/március, 150 - 152. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai bizonyítások, A háromszögek nevezetes pontjai, Sokszögek súlypontjának koordinátái, Feladat
Hivatkozás(ok):	Feladatok: 2006/december: B.3959

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jelölje $S$ az $A_{1} A_{2} A_{3}$ háromszög súlypontját, $F_{i}$ pedig az $A_{j} A_{k}$ oldal felezőpontját.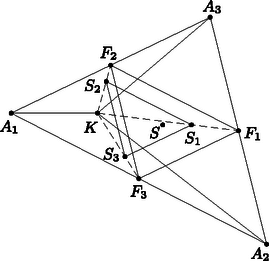

Mivel

F_{i} F_{j}

A_{1} A_{2} A_{3} ▵

középvonala, az

F_{i} F_{j}

párhuzamos

A_{i} A_{j}

-vel, és fele olyan hosszú. Emiatt az

A_{1} A_{2} A_{3} ▵

-et egy

S

középpontú,

λ_{1} = - \frac{1}{2}

arányú hasonlósági transzformáció az

F_{1} F_{2} F_{3} ▵

-be viszi.
Ugyanakkor

K S_{i} = 2 S_{i} F_{i}

, és a

K

S_{i}

F_{i}

pontok egy egyenesbe esnek. Emiatt az

F_{1} F_{2} F_{3} ▵

-et egy

K

középpontú,

λ_{2} = \frac{2}{3}

arányú hasonlósági transzformáció az

S_{1} S_{2} S_{3} ▵

-be viszi. Így az

S_{1} S_{2} S_{3}

háromszög oldalai párhuzamosak az

A_{1} A_{2} A_{3}

háromszög megfelelő oldalaival, ezért az

A_{1} A_{2} A_{3}

háromszöget egy (

λ_{3} = λ_{1} \cdot λ_{2} = - \frac{1}{2} \cdot \frac{2}{3} = - \frac{1}{3}

arányú) középpontos hasonlóság viszi át az

S_{1} S_{2} S_{3}

háromszögbe, tehát a hasonlóság középpontján az

A_{i} S_{i}

szakaszok áthaladnak.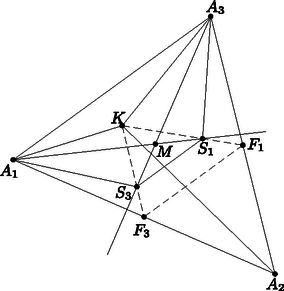

II. megoldás.

F_{1} F_{3}

A_{1} A_{2} A_{3} ▵

középvonala, így

F_{1} F_{3} = \frac{A_{1} A_{3}}{2}

és a két szakasz párhuzamos. Tudjuk, hogy a súlypont a súlyvonal oldalhoz közelebbi harmadolópontja. Ezek alapján a

K F_{1} F_{3} ▵

-ben a párhuzamos szelőszakaszok tételének megfordítása miatt:

\begin{matrix} S_{1} S_{3} = \frac{2}{3} F_{1} F_{3} = \frac{2}{6} A_{1} A_{3}, \end{matrix}

és

S_{1} S_{3} ∥ F_{1} F_{3}

II. megoldás. Ezekből következik, hogy

A_{1} S_{3} S_{1} A_{3}

trapéz, és alapjainak aránya

\begin{matrix} S_{1} S_{3} : A_{1} A_{3} = 1 : 3. \end{matrix}

Tudjuk, hogy a trapéz átlói az alapok arányában osztják egymást, vagyis

S_{3} M : M A_{3} = S_{1} M : M A_{1} = 1 : 3

Hasonló gondolatmenettel belátható, hogy

A_{1} S_{2} S_{1} A_{2}

trapéz, és átlóinak metszéspontját

N

-nel jelölve

S_{2} N : N A_{2} = S_{1} N : N A_{1} = 1 : 3

.
Mivel

S_{1} M : M A_{1} = S_{1} N : N A_{1} = 1 : 3

, azért

M = N

, tehát a három szakasz valóban egy ponton halad át.

III. megoldás. Tekintsünk a síkon egy tetszőleges

O

pontot, és indítsunk vektorokat

O

-ból az

A_{i}

S_{i}

illetve

K

pontokba. A vektorokat jelöljük a megfelelő kisbetűkkel.
Mivel

S_{i}

K A_{j} A_{k}

háromszög súlypontja, a következőképpen írható fel vektorokkal:

\begin{matrix} s_{i} = \frac{a_{j} + a_{k} + k}{3} . \end{matrix}

Tekintsük az

A_{i} S_{i}

szakaszok

S_{i}

-hez közelebbi negyedelőpontját, melyet jelöljön

P

. A

P

pontba mutató vektor így írható fel:

\begin{matrix} p = \frac{a_{i} + 3 s_{i}}{4} = \frac{a_{i} + 3 (\frac{a_{j} + a_{k} + k}{3})}{4} = \frac{a_{i} + a_{j} + a_{k} + k}{4} . \end{matrix}

Ez független

i

választásától, tehát az

A_{i} S_{i}

szakaszok

S_{i}

-hez közelebbi negyedelőpontja

i

mindhárom értékére

P

. A három egyenes valóban egy ponton megy át.

Megjegyzések. 1. A következő gondolatmenettel található ki, hogy a negyedelőpont lesz a közös metszéspont: Ha találunk olyan

(p_{i}, q_{i})

(p_{j}, q_{j})

(p_{k}, q_{k})

számpárokat, melyekben a számok összege 1, és teljesül, hogy az

a_{i}

\frac{a_{j} + a_{k} + k}{3}

vektorok

p_{i}

-vel és

q_{i}

-vel vett lineáris kombinációja megegyezik

a_{j}

\frac{a_{i} + a_{k} + k}{3}

vektorok

p_{j}

-vel és

q_{j}

-vel vett lineáris kombinációjával, illetve az

a_{k}

\frac{a_{i} + a_{j} + k}{3}

vektorok

p_{k}

-val és

q_{k}

-val vett lineáris kombinációjával, akkor ez a közös lineáris kombináció mindhárom szakaszra illeszkedik. A

(p_{i}, q_{i}) = (p_{j}, q_{j}) = (p_{k}, q_{k}) = (\frac{1}{4}, \frac{3}{4})

számpárok megfelelőek, a közös lineáris kombináció a szakaszok negyedelőpontja.
2. Többen koordinátageometriával oldották meg a feladatot. Kiszámították például, hogy

A_{1} S_{1}

és

A_{2} S_{2}

, illetve

A_{1} S_{1}

és

A_{3} S_{3}

metszéspontjának koordinátái megegyeznek.

IV. megoldás. A feladat megoldásához hívjuk segítségül a fizikát. Helyezzünk egységnyi, például 1 kg-os tömegű pontszerű testeket az

A_{1}

A_{2}

A_{3}

K

pontokba. A rendszer helyettesíthető egy

P

-be, a rendszer tömegközéppontjába helyezett 4 kg-os testtel.
Tekintsük először az

A_{1}

A_{2}

K

pontokat. Ez a rendszer az egyenlő tömegek miatt egy

S_{3}

-ba helyezett 3 kg-os testtel helyettesíthető. A rendszer és így az

A_{3}

-ba és

S_{3}

-ba helyezett testek tömegközéppontja

P

, és két test tömegközéppontja rajta van a pontok egyenesén, ezért

P

illeszkedik

A_{3} S_{3}

-ra. Hasonlóan láthatjuk be, hogy

P

illeszkedik

A_{2} S_{2}

-re és

A_{1} S_{1}

-re is. Ezzel a feladat állítását beláttuk.

Megjegyzés. Még többet is beláthatunk ennek a modellnek a segítségével. Támasszuk alá az

A_{3} S_{3}

szakaszt. A rendszer pontosan akkor lesz egyensúlyban, ha a tömegközéppontjánál támasztottuk alá. Ekkor lesz a forgatónyomatékok eredője 0. Tehát

A_{3} P \cdot 1 = P S_{3} \cdot 3

, amiből

\frac{A_{3} P}{P S_{3}} = 3

, tehát

P

negyedeli az

A_{3} S_{3}

, és hasonlóan az

A_{2} S_{2}

és az

A_{1} S_{1}

szakaszt.