Feladat: B.3925 Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Csizmadija Laura ,  Horváth Bálint ,  Mester Anita ,  Ősz Edina ,  Tasnádi Borbála 
Füzet: 2008/március, 143 - 147. oldal  PDF  |  MathML 
Témakör(ök): Síkgeometriai bizonyítások, Középponti és kerületi szögek, Tengelyes tükrözés, Koszinusztétel alkalmazása, Feladat
Hivatkozás(ok):Feladatok: 2006/szeptember: B.3925

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. Mindegyik megoldásban azt az esetet vizsgáljuk, amikor BC>AB, és így F∈BC^, tehát T∈BC. Ha pedig BC=AB, akkor B=F, T az AC felezőpontja, így az állítás triviális.

 
I. megoldás. Mivel F az ABC^ ív felezőpontja, azért FA^=FC^, és így FA=FC. Ebből a kerületi szögek tétele miatt FAC∢=FCA∢, amit jelöljön α. Ebből következik, hogy AFC∢=180∘-2α.
Ismét a kerületi szögek tétele miatt FBC∢=FAC∢=α, valamint ABC∢=AFC∢=180∘-2α, így ABF∢=180∘-α.
 
 

Az AFB háromszögben a koszinusz-tételt felírva kapjuk, hogy:
FA2=AB2+BF2-2⋅AB⋅BF⋅cos(180∘-α),
ahonnan FC=FA miatt
FC2=AB2+BF2+2⋅AB⋅BF⋅cosα.(1)

A TBF derékszögű háromszögben cosα=BTBF, és így
BF⋅cosα=BT.(2)

A TCF és a BTF derékszögű háromszögekben a Pitagorasz-tétel szerint
FC2=TC2+TF2,(3)
illetve
BF2=BT2+TF2.(4)

A (3), (4) és (2) egyenletek jobb oldalát (1)-ben a megfelelő helyre beírva kapjuk, hogy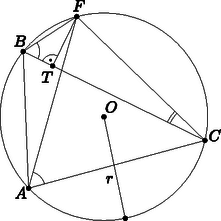
TC2+TF2=AB2+BT2+TF2+2⋅AB⋅BT,
ahonnan
TC2=AB2+2⋅AB⋅BT+BT2=(AB+BT)2,
és így valóban TC=AB+BT.
 
II. megoldás. Jelölje a körív sugarát r, a CBF szöget α, a BCF szöget pedig β.
 
 

A feladat feltétele, valamint a kerületi szögek tétele miatt FBC∢=FAC∢=FCA∢=α. Tudjuk még, hogy BCA∢=α-β. Ezek alapján:
FC=2rsinα,FB=2rsinβ,BA=2rsin(α-β).


Ezt felhasználva a CTF derékszögű háromszögben
CT=FC⋅cosβ=2r⋅sinαcosβ,
illetve a BTF derékszögű háromszögben
BT=FB⋅cosα=2rcosαsinβ.

Azt szeretnénk bebizonyítani, hogy CT=CB+BA2. Mivel BC=CT+TB, ez az egyenlőség ekvivalens a következővel: CT=TB+BA. A három szakasz hosszára kapott kifejezéseket az egyenlőségbe behelyettesítve kapjuk, hogy:
2rsinαcosβ=2rcosαsinβ+2rsin(α-β),
vagyis
sinαcosβ=cosαsinβ+sinαcosβ-cosαsinβ,
ami azonosság. Mivel a helyettesítés során is ekvivalens lépést végeztünk, ezzel bebizonyítottuk, hogy CT=CB+BA2.
 
III. megoldás. A feladat szerint ABF^=FC^, ezért AF=FC. Az AOC szöget 2α-val jelölve a kerületi szögek tétele szerint AFC∢=ABC∢=α. Az ACF▵ egyenlő szárú, ezért FO felezi az AFC szöget, azaz AFO∢=OFC∢=α2.
 
 

Tükrözzük a B pontot a T pontra, a kapott pont legyen B'. Ekkor a BB'F▵ egyenlő szárú, így BF=B'F és FBB'∢=FB'B∢.
Azt kell bizonyítani, hogy AB+BT=TB'+B'C. A tükrözés miatt BT=B'T, ezért elég belátni, hogy AB=B'C.
Az ACO háromszög egyenlő szárú az AO=OC miatt, így
OAC∢=OCA∢=180∘-2α2=90∘-α.

Az FAO háromszög is egyenlő szárú, FO=OA, tehát
OFA∢=FAO∢=α2.
Innen
FAC∢=FAO∢+OAC∢=90∘-α+α2=90∘-α2.
A kerületi szögek tétele és az eddigiek miatt:
90∘-α2=FAC∢=FBC∢=FBB'∢=FB'B∢,
és így
FB'C∢=180∘-FB'B∢=90∘+α2,ABF∢=α+(90∘-α2)=90∘+α2.

Mivel AF=CF, BF=B'F és ABF∢=FB'C∢=90∘+α2, a B'CF és a BAF háromszögeknek megegyezik két oldala és a nagyobbikkal szemközti szöge, tehát a két háromszög egybevágó. Ebből következik, hogy a harmadik oldaluk is egyenlő, vagyis AB=B'C.
Ezzel az állítást beláttuk.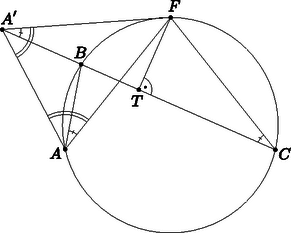
 
IV. megoldás. Mivel F az AC körív felezőpontja, azért FA=FC. Forgassuk el F körül az A pontot úgy, hogy a kapott A' pont a BC szakasz által meghatározott egyenesre kerüljön. A forgatás távolságtartó, ezért FA=FA'. A két egyenlőséget egybevetve FC=FA', tehát az A'CF▵ egyenlő szárú és A'CF∢=CA'F∢. Jelölje ezt a szöget α. A kerületi szögek tétele miatt BAF∢=BCF∢=α. Az AA'F▵ egyenlő szárú, mert FA=FA'. A háromszögben AA'F∢=A'AF∢. Jelölje ezt a szöget β.
 
 

Ekkor BA'A∢=β-α, és A'AB∢=β-α, ezért az ABA'▵ egyenlő szárú és így AB=A'B. Ez azt jelenti, hogy a töröttvonal hossza A'C, mert A'C=A'B+BC, és A'B=AB.
Az A'CF▵ egyenlő szárú, tehát FT felezi az alapját, A'C-t.
Ezzel beláttuk, hogy a T pont felezi a töröttvonal hosszát.
 
V. megoldás. Jelölje a BC szakasz felező merőlegesét t. Tükrözzük az F és a T pontot t-re, a tükörképek legyenek rendre F' és T'.
A TT'F'F négyszög egy derékszögű, szimmetrikus trapéz, vagyis egy téglalap. Ebből következik, hogy 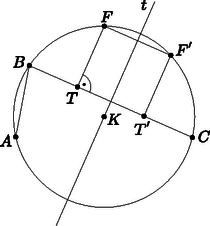TT'=FF'.
 
 

A tükrözés miatt BT=CT' és BF^=CF'^. Mivel F az ABC^ ív felezőpontja, AF^=CF^. Így AF^-BF^=CF^-CF'^, vagyis AB^=FF'^. Egy körben egyenlő hosszúságú ívekhez egyenlő hosszúságú húrok tartoznak, ezért AB=FF'.
A fentiek alapján AB+BT=FF'+CT'=TT'+CT'=CT, vagyis valóban egyenlőek a megfelelő szakaszok.
 
Megjegyzés. Ez a feladat már Eukleidész Elemek című művében is szerepelt.