Kezdőlap


Feladat:	C.902	Korcsoport: 16-17	Nehézségi fok: könnyű
Megoldó(k):	Buza Dániel István , Englert Ákos , Lantos Tamás
Füzet:	2008/március, 139 - 141. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai szerkesztések, Pitagorasz-tétel alkalmazásai, Kör geometriája, Kör egyenlete, C gyakorlat
Hivatkozás(ok):	Feladatok: 2007/május: C.902

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Használjuk az 1. ábra jelöléseit. Legyen a feltételeknek megfelelő húr hossza $3 x = A E$ , távolsága a nagyobbik kör $O$ középpontjától $y = C O$ . Legyen a nagy kör sugara $r$ , a kis kör sugara ekkor 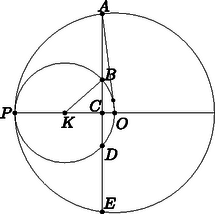$\frac{1}{2} r$ .

1. ábra

Tudjuk, hogy

A B = B D = D E

B C = \frac{1}{2} B D

, és így

A C = 3 B C

. A

B K C

háromszögre felírva Pitagorasz tételét:

\begin{matrix} B C^{2} & = B K^{2} - C K^{2}, & (1) \\ B C & = \sqrt[]{{(\frac{1}{2} r)}^{2} - {(\frac{1}{2} r - y)}^{2}} . \end{matrix}

A O C

háromszögre felírva a Pitagorasz-tételt:

\begin{matrix} A C^{2} = A O^{2} - C O^{2}, A C = \sqrt[]{r^{2} - y^{2}} . \end{matrix}

(2)

A C = 3 B C

egyenlőségbe (1) és (2) jobb oldalát beírva, majd négyzetre emelve:

\begin{matrix} r^{2} - y^{2} = 9 [\frac{1}{4} r^{2} - (\frac{1}{4} r^{2} - r y + y^{2})], ahonnan - 8 y^{2} + 9 r y - r^{2} = 0. \end{matrix}

Ezt

y

-ra megoldva:

\begin{matrix} y_{1,2} = \frac{- 9 r \pm 7 r}{- 16}, y_{1} = \frac{1}{8} r, y_{2} = r . \end{matrix}

y_{2}

nem megoldás, hiszen ekkor a ,,húr'' a két kör érintkezési pontja lenne.
Tehát a keresett húr a

P O

szakaszra az

O

-hoz közelebbi nyolcadoló pontjában emelt merőleges.

II. megoldás. Jelöljük a körök által a keresett egyenesből levágott egyenlő hosszúságú részek hosszát

2 m

-mel.
A 2. ábrán látható

A B C

és

B D E

háromszögek Thalész tétele alapján derékszögűek. A derékszögű háromszögeket az átfogóhoz tartozó magasság hasonló háromszögekre osztja, s így adódik, hogy az átfogóhoz tartozó magasság négyzete egyenlő az alap két részének szorzatával. Ezt a fenti két háromszögre alkalmazva

x (r - x) = m^{2}

és

(r + x) (r - x) = {(3 m)}^{2}

. Az első egyenlet 9-szeresét behelyettesítve a második jobb oldalába: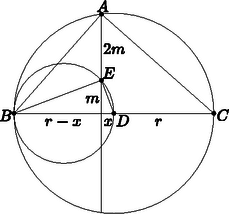

\begin{matrix} r^{2} - x^{2} = 9 x (r - x), innen 8 x^{2} - 9 r x + r^{2} = 0. \end{matrix}

Ennek megoldásai

x = r

és

x = \frac{r}{8}

, de a kettőből most is csak az utóbbi megfelelő.

2. ábra

Az egyenest tehát a nagy kör középpontjától a sugara

\frac{1}{8}

-ánál kell meghúznunk. A nyolcadolás szakaszfelezésekkel megoldható.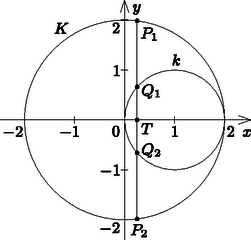

Megjegyzés. A használt tétel az ún. magasságtétel. Ugyanezekkel az egyenletekkel kell számolni, ha valaki a körhöz belső pontból húzott szelőszakaszokra vonatkozó tételt használja fel.

III. megoldás. Legyen a

K

kör sugara

R

, a

k

köré pedig

r

. Helyezzük el a köröket egy olyan koordinátarendszerben a 3. ábrának megfelelően, amelyben

R = 2

K

középpontja az origó,

k

középpontja az

(1; 0)

pont, a körök középpontjára illeszkedő egyenes az

x

tengely. A keresett húr erre merőleges, egyenlete tehát

x = x_{0}

alakú, ahol

0 < x_{0} < 2

. Végpontjai legyenek

P_{1}

és

P_{2}

, a

k

körrel alkotott metszéspontok

Q_{1}

és

Q_{2}

, az

x

tengellyel vett metszéspont pedig

T

. Tudjuk, hogy

Q_{1}

és

Q_{2}

P_{1} P_{2}

szakasz harmadolópontjai,

T

felezi a

Q_{1} Q_{2}

szakaszt, így

3 T Q_{1} = T P_{1}

3. ábra

Írjuk fel a két kör egyenletét, majd a fenti egyenlőséget felhasználva számoljuk ki

Q_{1}

és

P_{1}

közös abszcisszáját, amiről tudjuk, hogy pozitív.

K

egyenlete

x^{2} + y^{2} = 4,

ahonnan

y = \sqrt[]{4 - x^{2}}

k

egyenlete

{(x - 1)}^{2} + y^{2} = 1,

amiből

y = \sqrt[]{- x^{2} + 2 x}

.
Azt az

x_{0}

számot keressük, amelyre

3 \cdot \sqrt[]{- x_{0}^{2} + 2 x_{0}} = \sqrt[]{4 - x_{0}^{2}}

.
Négyzetre emelve és rendezve:

\begin{matrix} 4 x_{0}^{2} - 9 x_{0} + 2 = 0. \end{matrix}

(1)

Az egyenlet megoldása a 2 és az

\frac{1}{4}

, de csak az utóbbi megfelelő. Tehát

x_{0} = \frac{1}{4}

Megjegyzés. Van egy további, igen meglepő szerkesztés is, amit a 4. ábra mutat.

4. ábra

3 r

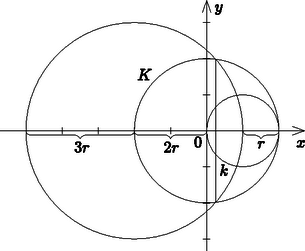sugarú kör, melynek középpontja a két adott kör középpontját összekötő egyenes és

K

metszéspontja, kimetszi

K

-ból a keresett húr két végpontját. Valóban: a kör egyenlete az előző koordináta-rendszerben:

{(x + 2)}^{2} + y^{2} = 9

, és a

K

kör

x^{2} + y^{2} = 4

egyenletéből:

\begin{matrix} P_{1} (\frac{1}{4}, \sqrt[]{4 - \frac{1}{16}}) = P_{1} (\frac{1}{4}, \sqrt[]{\frac{63}{16}}), \end{matrix}

ami kielégíti az (1) kör egyenletét.